
【題目】設(shè)函數(shù)![]() ,曲線
,曲線![]() 在點(
在點(![]() ,f(
,f(![]() ))處的切線與y軸垂直.
))處的切線與y軸垂直.
(1)求b.
(2)若![]() 有一個絕對值不大于1的零點,證明:
有一個絕對值不大于1的零點,證明:![]() 所有零點的絕對值都不大于1.
所有零點的絕對值都不大于1.
【答案】(1)![]() ;(2)證明見解析
;(2)證明見解析
【解析】
(1)利用導數(shù)的幾何意義得到![]() ,解方程即可;
,解方程即可;
(2)由(1)可得![]() ,易知
,易知![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() ,
,![]() 上單調(diào)遞增,且
上單調(diào)遞增,且![]() ,采用反證法,推出矛盾即可.
,采用反證法,推出矛盾即可.
(1)因為![]() ,
,
由題意,![]() ,即
,即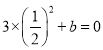
則![]() ;
;
(2)由(1)可得![]() ,
,
![]() ,
,
令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() ,
,![]() 上單調(diào)遞增,
上單調(diào)遞增,
且![]() ,
,
若![]() 所有零點中存在一個絕對值大于1的零點
所有零點中存在一個絕對值大于1的零點![]() ,則
,則![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
當![]() 時,
時,![]() ,
,
又![]() ,
,
由零點存在性定理知![]() 在
在![]() 上存在唯一一個零點
上存在唯一一個零點![]() ,
,
即![]() 在
在![]() 上存在唯一一個零點,在
上存在唯一一個零點,在![]() 上不存在零點,
上不存在零點,
此時![]() 不存在絕對值不大于1的零點,與題設(shè)矛盾;
不存在絕對值不大于1的零點,與題設(shè)矛盾;
當![]() 時,
時,![]() ,
,
又![]() ,
,
由零點存在性定理知![]() 在
在![]() 上存在唯一一個零點
上存在唯一一個零點![]() ,
,
即![]() 在
在![]() 上存在唯一一個零點,在
上存在唯一一個零點,在![]() 上不存在零點,
上不存在零點,
此時![]() 不存在絕對值不大于1的零點,與題設(shè)矛盾;
不存在絕對值不大于1的零點,與題設(shè)矛盾;
綜上,![]() 所有零點的絕對值都不大于1.
所有零點的絕對值都不大于1.
【點晴】
本題主要考查利用導數(shù)研究函數(shù)的零點,涉及到導數(shù)的幾何意義,反證法,考查學生邏輯推理能力,是一道有一定難度的題.


科目:高中數(shù)學 來源: 題型:
【題目】![]() 是自然對數(shù)的底數(shù),
是自然對數(shù)的底數(shù),![]() ,已知函數(shù)
,已知函數(shù)![]() ,
,![]() .
.
(1)若函數(shù)![]() 有零點,求實數(shù)
有零點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)對于![]() ,證明:當
,證明:當![]() 時,
時,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知三棱柱ABC–A1B1C1的底面是正三角形,側(cè)面BB1C1C是矩形,M,N分別為BC,B1C1的中點,P為AM上一點.過B1C1和P的平面交AB于E,交AC于F.
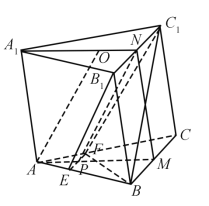
(1)證明:AA1//MN,且平面A1AMN⊥平面EB1C1F;
(2)設(shè)O為△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=![]() ,求四棱錐B–EB1C1F的體積.
,求四棱錐B–EB1C1F的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() 且橢圓的短軸長為
且橢圓的短軸長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知動直線![]() 過右焦點
過右焦點![]() ,且與橢圓
,且與橢圓![]() 分別交于
分別交于![]() 兩點.試問
兩點.試問![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得,
,使得,![]() 恒成立?若存在求出點
恒成立?若存在求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的極小值;
的極小值;
(Ⅱ)當![]() 時,討論
時,討論![]() 的單調(diào)性;
的單調(diào)性;
(Ⅲ)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有且只有一個零點,求
上有且只有一個零點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2019年6月25日,《固體廢物污染環(huán)境防治法(修訂草案)》初次提請全國人大常委會審議,草案對“生活垃圾污染環(huán)境的防治”進行了專項規(guī)定.某小區(qū)采取一系列措施,宣傳垃圾分類的知識與意義,并采購分類垃圾箱.為了了解垃圾分類的效果,該小區(qū)物業(yè)隨機抽取了200位居民進行問卷調(diào)查,每位居民對小區(qū)采取的措施給出“滿意”或“不滿意”的評價.根據(jù)調(diào)查結(jié)果統(tǒng)計并做出年齡分布條形圖和持不滿意態(tài)度的居民的結(jié)構(gòu)比例圖,如圖,在這200份問卷中,持滿意態(tài)度的頻率是0.65.
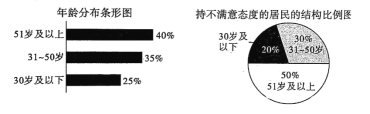
(1)完成下面的![]() 列聯(lián)表,并判斷能否有
列聯(lián)表,并判斷能否有![]() 的把握認為“51歲及以上”和“50歲及以下”的居民對該小區(qū)采取的措施的評價有差異
的把握認為“51歲及以上”和“50歲及以下”的居民對該小區(qū)采取的措施的評價有差異
滿意 | 不滿意 | 總計 | |
51歲及以上的居民 | |||
50歲及以下的居民 | |||
總計 | 200 |
(2)按“51歲及以上”和“50歲及以下”的年齡段采取分層抽樣的方法從中隨機抽取5份,再從這5份調(diào)查問卷中隨機抽取2份進行電話家訪,求電話家訪的兩位居民恰好一位年齡在51歲及以上,另一位年齡在50歲及以下的概率.
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附表及參考公式: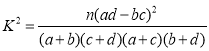 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() 是邊長為2的等邊三角形,且
是邊長為2的等邊三角形,且![]() ,
,![]() ,點
,點![]() 是棱
是棱![]() 上的動點.
上的動點.
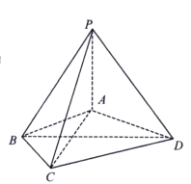
(I)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)當線段![]() 最小時,求直線
最小時,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對于定義城為R的函數(shù)![]() ,若滿足:①
,若滿足:①![]() ;②當
;②當![]() ,且
,且![]() 時,都有
時,都有![]() ;③當
;③當![]() 且
且![]() 時,都有
時,都有![]() ,則稱
,則稱![]() 為“偏對稱函數(shù)”.下列函數(shù)是“偏對稱函數(shù)”的是( )
為“偏對稱函數(shù)”.下列函數(shù)是“偏對稱函數(shù)”的是( )
A.![]() B.
B.![]()
C.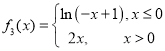 D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
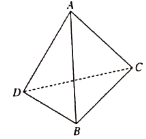
【題目】現(xiàn)有一副斜邊長為10的直角三角板,將它們斜邊![]() 重合,若將其中一個三角板沿斜邊折起形成三棱錐
重合,若將其中一個三角板沿斜邊折起形成三棱錐![]() ,如圖所示,已知
,如圖所示,已知![]() ,
,![]() ,則三棱錐
,則三棱錐![]() 的外接球的表面積為______;該三棱錐體積的最大值為_______.
的外接球的表面積為______;該三棱錐體積的最大值為_______.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com