給定有限單調遞增數列{xn}(n∈N*,n≥2)且xi≠0(1≤i≤n),定義集合A={(xi,xj)|1≤i,j≤n,且i,j∈N*}.若對任意點A1∈A,存在點A2∈A使得OA1⊥OA2(O為坐標原點),則稱數列{xn}具有性質P.
(I)判斷數列{xn}:-2,2和數列{yn}:-2,-l,1,3是否具有性質P,簡述理由.
(II)若數列{xn}具有性質P,求證:
①數列{xn}中一定存在兩項xi,xj使得xi+xj=0:
②若x1=-1,xn>0且xn>1,則x2=l.
【答案】
分析:(Ⅰ)數列{x
n}具有性質P,數列{y
n}不具有性質P,利用新定義驗證即可得到結論;
(II)①取A
1(x
k,x
k),根據數列{x
n}具有性質P,可得存在點A
2(x
i,x
j)使得OA
1⊥OA
2,即x
kx
i+x
kx
j=0,從而可得結論;
②由①知,數列{x
n}中一定存在兩項x
i,x
j,使得x
i+x
j=0,根據數列是單調遞增數列且x
2>0,可得1為數列中的一項,利用反證法,即可得到結論.
解答:(Ⅰ)解:數列{x
n}具有性質P,數列{y
n}不具有性質P.
對于數列{x
n},若A
1(-2,2),則A
2(2,2);若A
1(-2,-2),則A
2(2,-2),∴具有性質P;
對于數列{y
n},當A
1(-2,3),若存在A
2(x,y)滿足OA
1⊥OA
2,即-2x+3y=0,
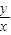
=

,數列{y
n}中不存在這樣的數x、y,
∴不具有性質P.
(II)證明:①取A
1(x
k,x
k),∵數列{x
n}具有性質P,∴存在點A
2(x
i,x
j)使得OA
1⊥OA
2,即x
kx
i+x
kx
j=0,
∵x
k≠0,∴x
i+x
j=0.
②由①知,數列{x
n}中一定存在兩項x
i,x
j,使得x
i+x
j=0.
又數列是單調遞增數列且x
2>0,∴1為數列中的一項,
假設x
2≠1,則存在k(2<k<n,k∈N
*),有x
k=1,∴0<x
2<1,
此時取A
1(x
2,x
n),數列{x
n}具有性質P,
∴存在點A
2(x
t,x
s)使得OA
1⊥OA
2,
∴x
2x
t+x
nx
s=0
所以x
t=-1時,x
2=x
nx
s>x
s≥x
2,矛盾;x
s=-1時,
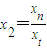
≥1,矛盾,所以x
2=1.
點評:本題考查新定義,考查反證法的運用,考查學生分析解決問題的能力,難度較大.

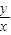 =
= ,數列{yn}中不存在這樣的數x、y,
,數列{yn}中不存在這樣的數x、y,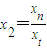 ≥1,矛盾,所以x2=1.
≥1,矛盾,所以x2=1.

 閱讀快車系列答案
閱讀快車系列答案