【答案】
分析:(1)分別令x
1=x
2=0,x
1=1,x
2=0,f(x
)=f(1),又因為f(x)為單調函數,從而可求x
的值;
(2)由(1)得f(x
1+x
2)=f(x
1)+f(x
2)+1,令x
1=n,x
2=1,f(n+1)=f(n)+f(1)+1=f(n)+2,f(n)=2n-1.故可求a
n進而可有
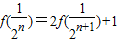
,從而可求通項,故可證;
(3)構造函數F(n)=a
n+1+a
n+2+…+a
2n,證明n≥2時,為單調減函數,從而可求x的取值范圍.
解答:解:(1)令x
1=x
2=0⇒f(x
)=-f(0).又令x
1=1,x
2=0,f(1)=-f(0).
∴f(x
)=f(1),由函數f(x)單調性知,x
=1.
(2)由(1)知,f(x
1+x
2)=f(x
1)+f(x
2)+f(1)=f(x
1)+f(x
2)+1,
由x
1,x
2的任意性,令x
1=n,x
2=1,f(n+1)=f(n)+f(1)+1=f(n)+2,
∴f(n)=2n-1.(n∈N
*).
∴
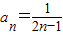
.
又∵
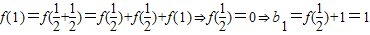
.
又∵
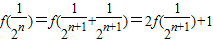
,
∴
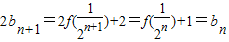
.
∴
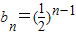
.
由數列求和方法知:
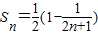
,
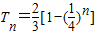
.∴
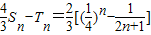
.
∵4
n=(3+1)
n=C
nn3
n+C
nn-13
n-1+…+C
n13+C
n≥3n+1>2n+1,∴

.
(3)令F(n)=a
n+1+a
n+2+…+a
2n⇒F(n+1)-F(n)=a
2n+1+a
2n+2-a
n+1=
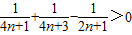
(通分易證)∴當n≥2時,
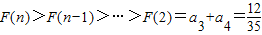
.
∴
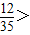
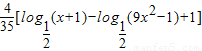
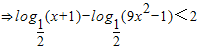
.
解此不等式,所以x的取值范圍為
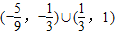
.
點評:本題以新定義為載體,考查抽象函數,考查賦值法,同時考查構造函數,利用函數的單調性解決恒成立問題.

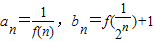 ,記Sn=a1a2+a2a3+…+anan+1,Tn=b1b2+b2b3+…+bnbn+1,比較
,記Sn=a1a2+a2a3+…+anan+1,Tn=b1b2+b2b3+…+bnbn+1,比較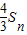 與Tn的大小關系,并給出證明;
與Tn的大小關系,并給出證明;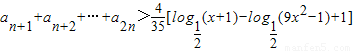 對任意不小于2的正整數n都成立,求x的取值范圍.
對任意不小于2的正整數n都成立,求x的取值范圍.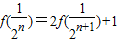 ,從而可求通項,故可證;
,從而可求通項,故可證;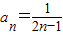 .
.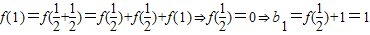 .
.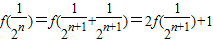 ,
,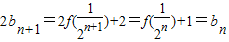 .
.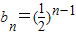 .
.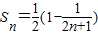 ,
,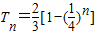 .∴
.∴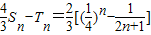 .
. .
.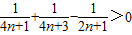 (通分易證)∴當n≥2時,
(通分易證)∴當n≥2時,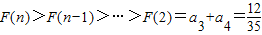 .
.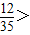
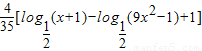
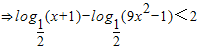 .
.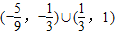 .
.
