解:(1)由
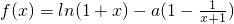
知定義域:{x|x>-1}
對f(x)求導得:
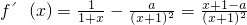
①在a≤0時,有x+1-a>0恒成立.故f(x)>0
故此時f(x)在(-1,+∞)上單調遞增
②在a>0時,由f'(x)=0知x=a-1
| x | (-1,a-1) | a-1 | (a-1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↓ | 極小值 | ↑ |
故在a>0時,f(x)在(-1,a-1)上為減函數,在[a-1,+∞)上為增函數.
因此函數在a≤0時,在(-1,+∞)上單調遞增;在a>0時,f(x)在(-1,a-1)上為減函數,在[a-1,+∞)上為增函數.…
(2)要證明:
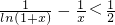
在(0,1)上成立.
只需證:
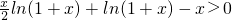
,在(0,1)上恒成立
設
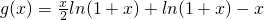
則
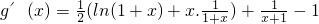
=

由(1)可知a=1,f(x)在x=0時取到最小值
有
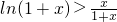
,在x>0時恒成立.
從而可知g'(x)>0,故g(x)在(0,1)上為增函數∴g(x)>g(0)=0
即:
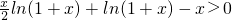
恒成立,從而原不等式得證.…
分析:(1)先求函數的定義域,然后求出導函數,討論a的正負,再結合導函數的符號可得函數f(x)的單調區間;
(2)用分析法進行證明,要證明:
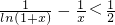
在(0,1)上成立,只需證:
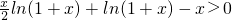
,在(0,1)上恒成立,設
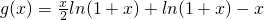
,然后利用導數研究函數g(x)在(0,1)上單調性,可得結論.
點評:本題主要考查了函數恒成立問題,以及利用導數研究函數單調性,同時考查了轉化能力,屬于中檔題.

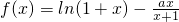 (其中a為常數),求函數f(x)的單調區間;
(其中a為常數),求函數f(x)的單調區間;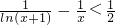 在0<x<1上恒成立.
在0<x<1上恒成立.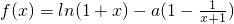 知定義域:{x|x>-1}
知定義域:{x|x>-1}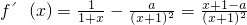
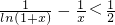 在(0,1)上成立.
在(0,1)上成立.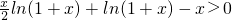 ,在(0,1)上恒成立
,在(0,1)上恒成立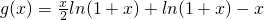
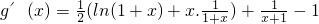 =
=
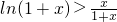 ,在x>0時恒成立.
,在x>0時恒成立.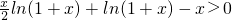 恒成立,從而原不等式得證.…
恒成立,從而原不等式得證.…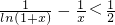 在(0,1)上成立,只需證:
在(0,1)上成立,只需證: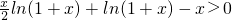 ,在(0,1)上恒成立,設
,在(0,1)上恒成立,設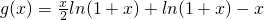 ,然后利用導數研究函數g(x)在(0,1)上單調性,可得結論.
,然后利用導數研究函數g(x)在(0,1)上單調性,可得結論.

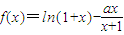 (其中a為常數),求函數f(x)的單調區間;
(其中a為常數),求函數f(x)的單調區間;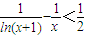 在0<x<1上恒成立.
在0<x<1上恒成立.