畫出以A(3,-1)、B(-1,1)、C(1,3)為頂點的△ABC的區域(包括各邊),寫出該區域所表示的二元一次不等式組,并求以該區域為可行域的目標函數z=3x-2y的最大值和最小值.
分析:本題考查的知識點是線性規劃,處理的思路為:根據已知的可行域,給出對應的約束條件,處理的方法遵循“線定界,點定域”,再使用角點法,求出目標函數的最大值.
解答: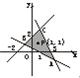
解:如圖,連接點A、B、C,
則直線AB、BC、CA所圍成的區域為所求△ABC區域.
∵直線AB的方程為x+2y-1=0,
BC及CA的直線方程分別為x-y+2=0,2x+y-5=0.
在△ABC內取一點P(1,1),分別代入x+2y-1,x-y+2,2x+y-5得:
+2y-1>0,x-y+2>0,2x+y-5<0.
因此所求區域的不等式組為
作平行于直線3x-2y=0的直線系3x-2y=t(t為參數),即平移直線y=
x,
觀察圖形可知:
當直線y=
x-
t過A(3,-1)時,縱截距-
t最小.
此時t最大,t
max=3×3-2×(-1)=11;
當直線y=
x-
t經過點B(-1,1)時,縱截距-
t最大,
此時t有最小值為t
min=3×(-1)-2×1=-5.
因此,函數z=3x-2y在約束條件下的最大值為11,最小值為-5.
點評:用圖解法解決線性規劃問題時,分析題目的已知條件,找出約束條件和目標函數是關鍵,可先將題目中的量分類、列出表格,理清頭緒,然后列出不等式組(方程組)尋求約束條件,并就題目所述找出目標函數.然后將可行域各角點的值一一代入,最后比較,即可得到目標函數的最優解.

 解:如圖,連接點A、B、C,
解:如圖,連接點A、B、C,

 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案 (必修3做)設計一個求
(必修3做)設計一個求 (必修3做)設計一個求
(必修3做)設計一個求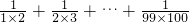 的值的程序框圖.
的值的程序框圖.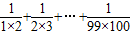 的值的程序框圖.
的值的程序框圖.