
【題目】某烘焙店加工一個成本為60元的蛋糕,然后以每個120元的價格出售,如果當天賣不完,剩下的這種蛋糕作餐廚垃圾處理.
(1)若烘焙店一天加工16個這種蛋糕,,求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]() (單位:個,
(單位:個,![]() )的函數解析式;
)的函數解析式;
(2)烘焙店記錄了100天這種蛋糕的日需求量(單位:個),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
頻數 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①若烘焙店一天加工16個這種蛋糕,![]() 表示當天的利潤(單位:元),求
表示當天的利潤(單位:元),求![]() 的分布列與數學期望及方差;
的分布列與數學期望及方差;
②若烘焙店一天加工16個或17個這種蛋糕,僅從獲得利潤大的角度考慮,你認為應加工16個還是17個?請說明理由.
【答案】(1)![]() (2)①分布列見解析;
(2)①分布列見解析;![]() (元);
(元);![]() ②應加工17個,詳見解析
②應加工17個,詳見解析
【解析】
(1)根據題意,分別討論![]() 和
和![]() 兩種情況,即可得出結果;
兩種情況,即可得出結果;
(2)①先由(1)計算出![]() 的可能取值,結合題中條件,即可得出分布列,進而可求出期望與方差;
的可能取值,結合題中條件,即可得出分布列,進而可求出期望與方差;
②根據題意求出![]() 的可能取值,得出期望,與①比較大小,即可得出結論.
的可能取值,得出期望,與①比較大小,即可得出結論.
(1)由題意,當![]() 時,利潤
時,利潤![]() ;
;
當![]() 時,利潤
時,利潤![]() ;
;
綜上,當天的利潤![]() 關于當天需求量
關于當天需求量![]() 的函數解析式為
的函數解析式為![]() ;
;
(2)①由(1)可得,
當![]() 時,利潤
時,利潤![]() ;
;
當![]() 時,利潤
時,利潤![]() ;
;
當![]() 時,利潤
時,利潤![]() ;
;
所以![]() 的分布列為:
的分布列為:
|
|
|
|
|
|
|
|
所以![]() (元);
(元);
![]() ;
;
②由題意,加工![]() 個蛋糕時,
個蛋糕時,
當![]() 時,利潤
時,利潤![]() ;
;
當![]() 時,利潤
時,利潤![]() ;
;
當![]() 時,利潤
時,利潤![]() ;
;
當![]() 時,利潤
時,利潤![]() ;
;
![]() 的分布列如下:
的分布列如下:
| 660 | 780 | 900 | 1020 |
| 0.1 | 0.2 | 0.16 | 0.54 |
則![]()
從數學期望來看,每天加工17個蛋糕的利潤高于每天加工16個蛋糕的利潤,應加工17個.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】第41屆世界博覽會于2010年5月1日至10月31日,在中國上海舉行,氣勢磅礴的中國館——“東方之冠”令人印象深刻,該館以“東方之冠,鼎盛中華,天下糧倉,富庶百姓”為設計理念,代表中國文化的精神與氣質.其形如冠蓋,層疊出挑,制似斗拱.它有四根高33.3米的方柱,托起斗狀的主體建筑,總高度為60.3米,上方的“斗冠”類似一個倒置的正四棱臺,上底面邊長是139.4米,下底面邊長是69.9米,則“斗冠”的側面與上底面的夾角約為( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接“五一國際勞動節”,某商場規定購買超過6000元商品的顧客可以參與抽獎活動現有甲品牌和乙品牌的掃地機器人作為獎品,從這兩種品牌的掃地機器人中各隨機抽取6臺檢測它們充滿電后的工作時長相關數據見下表(工作時長單位:分)
機器序號 | 1 | 2 | 3 | 4 | 5 | 6 |
甲品牌工作時長/分 | 220 | 180 | 210 | 220 | 200 | 230 |
乙品牌工作時長/分 | 200 | 190 | 240 | 230 | 220 | 210 |
(1)根據所提供的數據,計算抽取的甲品牌的掃地機器人充滿電后工作時長的平均數與方差;
(2)從乙品牌被抽取的6臺掃地機器人中隨機抽出3臺掃地機器人,記抽出的掃地機器人充滿電后工作時長不低于220分鐘的臺數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了豐富學生的課外文化生活,某中學積極探索開展課外文體活動的新途徑及新形式,取得了良好的效果.為了調查學生的學習積極性與參加文體活動是否有關,學校對200名學生做了問卷調查,列聯表如下:
參加文體活動 | 不參加文體活動 | 合計 | |
學習積極性高 | 80 | ||
學習積極性不高 | 60 | ||
合計 | 200 |
已知在全部200人中隨機抽取1人,抽到學習積極性不高的學生的概率為![]() .
.
(1)請將上面的列聯表補充完整;
(2)是否有99.9%的把握認為學習積極性高與參加文體活動有關?請說明你的理由;
(3)若從不參加文體活動的同學中按照分層抽樣的方法選取5人,再從所選出的5人中隨機選取2人,求至少有1人學習積極性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
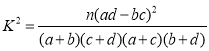 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的右頂點為
的右頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線與
的直線與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于另一個點
交于另一個點![]() ,且點
,且點![]() 在
在![]() 軸上的射影恰好為點
軸上的射影恰好為點![]() .
.
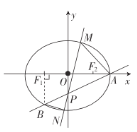
(1)求點![]() 的坐標;
的坐標;
(2)過點![]() 且斜率大于
且斜率大于![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點
兩點![]() ,若
,若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 過點
過點![]() ,過坐標原點
,過坐標原點![]() 作兩條互相垂直的射線與橢圓
作兩條互相垂直的射線與橢圓![]() 分別交于
分別交于![]() ,
,![]() 兩點.
兩點.
(1)證明:當![]() 取得最小值時,橢圓
取得最小值時,橢圓![]() 的離心率為
的離心率為![]() .
.
(2)若橢圓![]() 的焦距為2,是否存在定圓與直線
的焦距為2,是否存在定圓與直線![]() 總相切?若存在,求定圓的方程;若不存在,請說明理由.
總相切?若存在,求定圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】趙爽是我國漢代數學家、天文學家,他在注解《周髀算經》時,介紹了“勾股圓方圖”,亦稱“趙爽弦圖”,它被2002年國際數學家大會選定為會徽.“趙爽弦圖”是以弦為邊長得到的正方形,該正方形由4個全等的直角三角形加上中間一個小正方形組成類比“趙爽弦圖”,可類似地構造如圖所示的圖形它是由3個全等的三角形與中間的一個小等邊三角形拼成的一個大等邊三角形設DF=2AF=2,若在大等邊三角形中隨機取一點,則此點取自三個全等三角形(陰影部分)的概率是( )
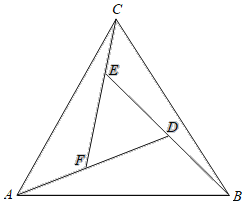
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com