
【題目】已知等差數(shù)列![]() 與數(shù)列
與數(shù)列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]()
![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)記![]() ,
,![]() 的前n項的和分別為
的前n項的和分別為![]() ,
,![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)令![]() ,可由
,可由![]() 求出
求出![]() ,進而求出
,進而求出![]() ,得到等差數(shù)列
,得到等差數(shù)列![]() 的通項公式,于是有
的通項公式,于是有![]() ,構造數(shù)列
,構造數(shù)列![]() ,設
,設![]() ,可變形得到
,可變形得到![]() ,求出
,求出![]() ,即可得數(shù)列
,即可得數(shù)列![]() 的通項公式.其它解法參考解析;
的通項公式.其它解法參考解析;
(2)要證![]() ,即證
,即證![]() ,根據(jù)
,根據(jù)![]() 的表達式可知其關于
的表達式可知其關于![]() 單調(diào)遞增,即證
單調(diào)遞增,即證![]() ,再通過放縮法即可證出,多種放縮方式見解析.
,再通過放縮法即可證出,多種放縮方式見解析.
(1)令![]() 有
有![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() .由
.由![]() 得
得![]() ,
,
設![]() ,則
,則![]() ,可得
,可得![]() ,
,
又![]() ,故
,故![]() ,則
,則![]() .
.
解法2:由![]() ,有
,有![]() ,(
,(![]() ),相減得
),相減得
![]() ,(
,(![]() ),
),
則![]() ,
,![]() ,……,
,……,![]() ,
,
相加得![]() ,則
,則![]() ,(
,(![]() ),
),
當![]() 時上式也成立.
時上式也成立.
又![]() 得
得![]() ,故
,故![]() .
.
解法3:由![]() 構造等比
構造等比![]() 也可以.
也可以.
(2)只需證![]() .
.
由(1)有![]() ,所以
,所以![]() ,記為
,記為![]() ,
,
而![]() ,所以
,所以![]() 單調(diào)遞增,
單調(diào)遞增,
有![]()
只需證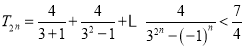 .
.
證法1:∵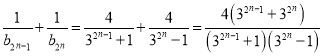
![]()
故![]()
![]() .
.
證法2:![]()
![]()
又![]()
則![]()
![]()
所以![]() .
.
證法3:∵ ,
,
∴![]()
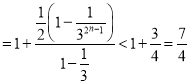 .
.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案科目:高中數(shù)學 來源: 題型:
【題目】設數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,若對任意
,若對任意![]() ,都有
,都有![]() ,則稱數(shù)列
,則稱數(shù)列![]() 具有性質(zhì)P.
具有性質(zhì)P.
(1)若數(shù)列![]() 是首項為1,公比為2的等比數(shù)列,試判斷數(shù)列
是首項為1,公比為2的等比數(shù)列,試判斷數(shù)列![]() 是否具有性質(zhì)P;
是否具有性質(zhì)P;
(2)若正項等差數(shù)列![]() 具有性質(zhì)P,求數(shù)列
具有性質(zhì)P,求數(shù)列![]() 的公差;
的公差;
(3)已知正項數(shù)列![]() 具有性質(zhì)P,
具有性質(zhì)P,![]() ,且對任意
,且對任意![]() ,有
,有![]() ,求數(shù)列
,求數(shù)列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 為奇函數(shù),且相鄰兩對稱軸間的距離為
為奇函數(shù),且相鄰兩對稱軸間的距離為![]() .
.
(1)求函數(shù)![]() 的最小正周期;
的最小正周期;
(2)將函數(shù)![]() 的圖象沿
的圖象沿![]() 軸方向向右平移
軸方向向右平移![]() 個單位長度,再把橫坐標變?yōu)樵瓉淼?/span>
個單位長度,再把橫坐標變?yōu)樵瓉淼?/span>![]() (縱坐標保持不變),得到函數(shù)
(縱坐標保持不變),得到函數(shù)![]() 的圖象,求函數(shù)
的圖象,求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)![]() 圖象上最高點與該最高點相鄰的圖象的對稱中心的距離為
圖象上最高點與該最高點相鄰的圖象的對稱中心的距離為![]() .
.
(1)求函數(shù)![]() 的最小正周期及單調(diào)遞增區(qū)間;
的最小正周期及單調(diào)遞增區(qū)間;
(2)把![]() 圖象上所有的點先橫坐標伸長為原來的
圖象上所有的點先橫坐標伸長為原來的![]() 倍(縱坐標不變),再向左平移
倍(縱坐標不變),再向左平移![]() 個單位得到函數(shù)
個單位得到函數(shù)![]() 的圖象.在
的圖象.在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分別是角
分別是角![]() ,
, ![]() ,
, ![]() 的對邊,若
的對邊,若![]() ,
, ![]() 的面積為
的面積為![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差數(shù)列,求
成等差數(shù)列,求![]() 的周長.
的周長.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
,![]() ,直線
,直線![]() :
:![]() (
(![]() 為參數(shù),
為參數(shù),![]() ).
).
(Ⅰ)求直線![]() 的普通方程;
的普通方程;
(Ⅱ)在曲線![]() 上求一點
上求一點![]() ,使它到直線
,使它到直線![]() 的距離最短,并求出點
的距離最短,并求出點![]() 的極坐標.
的極坐標.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com