
【題目】已知正方形ABCD的邊長為7,點M在AB上,點N在BC上,且AM=BN=3,現有一束光線從點M射向點N,光線每次碰到正方形的邊時反射,則這束光線從第一次回到原點M時所走過的路程為( )
A. ![]() B. 60 C.
B. 60 C. ![]() D. 70
D. 70
科目:高中數學 來源: 題型:
【題目】如圖,已知多面體ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.

(Ⅰ)證明:AB1⊥平面A1B1C1;
(Ⅱ)求直線AC1與平面ABB1所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】光伏發電是利用太陽能電池及相關設備將太陽光能直接轉化為電能,近幾年在國內出臺的光伏發電補貼政策的引導下,某地光伏發電裝機量急劇上漲,如下表:
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代碼 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
新增光伏裝機量 | 0.4 | 0.8 | 1.6 | 3.1 | 6.1 | 7.1 | 9.7 | 12.2 |
某位同學分別用兩種模型:①![]() ,②
,②![]() 進行擬合,得到相應的回歸方程并進行殘差分析,殘差圖如下(注:殘差等于
進行擬合,得到相應的回歸方程并進行殘差分析,殘差圖如下(注:殘差等于![]() )
)
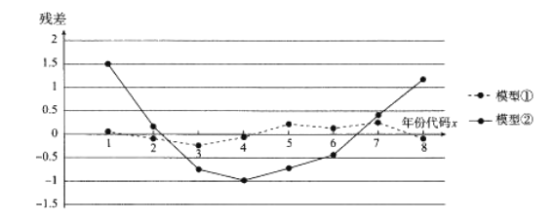
經過計算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)根據殘差圖,比較模型①,②的擬合效果,應該選擇哪個模型?并簡要說明理由.
(2)根據(1)的判斷結果及表中數據建立![]() 關于
關于![]() 的回歸方程,并預測該地區2020年新增光伏裝機量是多少.(在計算回歸系數時精確到0.01)
的回歸方程,并預測該地區2020年新增光伏裝機量是多少.(在計算回歸系數時精確到0.01)
附:歸直線的斜率和截距的最小二乘估計公式分別為: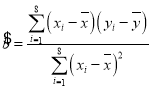 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知盒子中裝有紅色、藍色紙牌各100張,每種顏色紙牌均含標數為![]() 的紙牌各一張,兩種顏色紙牌的標數總和記為
的紙牌各一張,兩種顏色紙牌的標數總和記為![]() .
.
對于給定的正整數![]() ,若能從盒子中取出若干張紙牌,使其標數之和恰為
,若能從盒子中取出若干張紙牌,使其標數之和恰為![]() ,則稱其為一種取牌“n—方案”.記不同的n—方案種數為
,則稱其為一種取牌“n—方案”.記不同的n—方案種數為![]() .試求
.試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】武漢出現的新型冠狀病毒是一種可以通過飛沫傳播的變異病毒,某藥物研究所為篩查該新型冠狀病毒,需要檢驗血液是否為陽性,現有![]() 份血液樣本,每份樣本取到的可能性均等,有以下兩種檢驗方式:①逐份檢驗,則需要檢驗n次;②混合檢驗,將其中
份血液樣本,每份樣本取到的可能性均等,有以下兩種檢驗方式:①逐份檢驗,則需要檢驗n次;②混合檢驗,將其中![]() 份血液樣本分別取樣混合在一起檢驗.若檢驗結果為陰性,這k份血液全為陰性,因此這k份血液樣本檢驗一次就夠了,如果檢驗結果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份血液再逐份檢驗,此時這k份血液的檢驗次數總共為
份血液樣本分別取樣混合在一起檢驗.若檢驗結果為陰性,這k份血液全為陰性,因此這k份血液樣本檢驗一次就夠了,如果檢驗結果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份血液再逐份檢驗,此時這k份血液的檢驗次數總共為![]() 次.假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陰性還是陽性都是獨立的,且每份樣本是陽性結果的概率為
次.假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陰性還是陽性都是獨立的,且每份樣本是陽性結果的概率為![]() .
.
(1)假設有5份血液樣本,其中只有2份為陽性,若采取逐份檢驗方式,求恰好經過2次檢驗就能把陽性樣本全部檢驗出來的概率;
(2)現取其中![]() 份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的次數為
份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的次數為![]() ,采用混合檢驗方式,樣本需要檢驗的總次數為
,采用混合檢驗方式,樣本需要檢驗的總次數為![]() .
.
(i)試運用概率統計知識,若![]() ,試求P關于k的函數關系式
,試求P關于k的函數關系式![]() ;
;
(ii)若![]() ,采用混合檢驗方式可以使得這k份血液樣本需要檢驗的總次數的期望值比逐份檢驗的總次數期望值更少,求k的最大值.
,采用混合檢驗方式可以使得這k份血液樣本需要檢驗的總次數的期望值比逐份檢驗的總次數期望值更少,求k的最大值.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某一電視臺對年齡高于40歲和不高于40歲的人是否喜歡西班牙隊進行調查,40歲以上調查了50人,不高于40歲調查了50人,所得數據制成如下列聯表:
不喜歡西班牙隊 | 喜歡西班牙隊 | 總計 | |
40歲以上 |
|
| 50 |
不高于40歲 | 15 | 35 | 50 |
總計 |
|
| 100 |
已知工作人員從所有統計結果中任取一個,取到喜歡西班牙隊的人的概率為![]() ,則有超過________的把握認為年齡與西班牙隊的被喜歡程度有關.
,則有超過________的把握認為年齡與西班牙隊的被喜歡程度有關.
參考公式與臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函數f(x)在R上單調遞增,求實數a的取值范圍;
(3)是否存在實數a,使不等式f(x)≥2x-3對任意x∈R恒成立?若存在,求出a的取值范圍;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com