Question

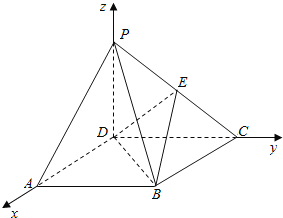
【題目】如圖，四棱錐P—ABCD的底面ABCD是正方形，側棱PD⊥底面ABCD，PD=DC，E是PC的中點．

（Ⅰ）證明PA//平面BDE；

（Ⅱ）求二面角B—DE—C的平面角的余弦值；

（Ⅲ）在棱PB上是否存在點F，使PB⊥平面DEF？證明你的結論．

Answer 1

【答案】（Ⅰ）證明見解析；（Ⅱ） ；（Ⅲ）證明見解析.

【解析】

（Ⅰ）以D為坐標原點，分別以DA、DC、DP所在直線為x軸、y軸、z軸建立空間直角坐標系，利用向量法能證明PA∥平面BDE；（Ⅱ）由已知求出平面BDE的一個法向量和平面DEC的一個法向量，利用向量法能求出二面角B﹣DE﹣C的余弦值；（Ⅲ）由已知得PB⊥DE，假設棱PB上存在點F，使PB⊥平面DEF，設，（0＜λ∠1），由此利用向量法能求出在棱PB上存在點F，PF=，使得PB⊥平面DEF．

（Ⅰ）證明：以D為坐標原點，

分別以DA、DC、DP所在直線為x軸、y軸、z軸建立空間直角坐標系，

設PD=DC=2，則A（2，0，0），P（0，0，2），E（0，1，1），B（2，2，0），

=（2，0，﹣2），=（0，1，1），，

設是平面BDE的一個法向量，

則由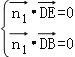，得，

取y=﹣1，得．

∵=2﹣2=0，∴，

又PA不包含于平面BDE，PA∥平面BDE；

（Ⅱ）由（Ⅰ）知=（1，﹣1，1）是平面BDE的一個法向量，

又==（2，0，0）是平面DEC的一個法向量．

設二面角B﹣DE﹣C的平面角為θ，

∴cosθ=cos＜，＞=．

故二面角B﹣DE﹣C的余弦值為．

（Ⅲ）∵=（2，2，﹣2），=（0，1，1），

∴=0，∴PB⊥DE，

假設棱PB上存在點F，使PB⊥平面DEF，設，（0＜λ∠1），

則=（2λ，2λ，﹣2λ），==（2λ，2λ，2﹣2λ），

由=0，得4λ2+4λ2﹣2λ（2﹣2λ）=0，

∴∈（0，1），此時PF=，

即在棱PB上存在點F，PF=，使得PB⊥平面DEF．