
如圖,四棱錐PABCD中,底面ABCD為平行四邊形,∠DAB=60°,AB=2AD,PD⊥底面ABCD。
(1)證明:PA⊥BD;(2)設PD=AD,求二面角A-PB-C的余弦值. 
(1)只需證明BD2+AD2=AB2;(2)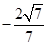 。
。
解析試題分析:(1)因為∠DAB=60°,AB=2AD,由余弦定理得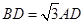 .
.
從而BD2+AD2=AB2,故BD⊥AD.
又PD⊥底面ABCD,可得BD⊥PD.
所以BD⊥平面PAD.故PA⊥BD. 6分
(2)如圖,以D為坐標原點,AD的長為單位長,射線DA為x軸的正半軸建立空間直角坐標系Dxyz.則A(1,0,0),B(0, ,0),C(-1,
,0),C(-1, ,0),P(0,0,1).
,0),P(0,0,1).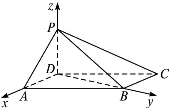
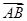 =(-1,
=(-1, ,0),
,0),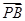 =(0,
=(0, ,-1),
,-1),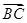 =(-1,0,0).
=(-1,0,0).
設平面PAB的法向量為n=(x,y,z),則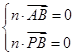
即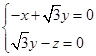
因此可取n=( ,1,
,1, ).
).
設平面PBC的法向量為m,則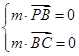
可取m=(0,-1,- ),
),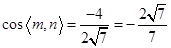 .
.
故二面角APBC的余弦值為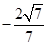 . 6分
. 6分
考點:線面垂直的判定定理;線面垂直的性質定理;二面角。
點評:二面角的求法是立體幾何中的一個難點。我們解決此類問題常用的方法有兩種:①綜合法,綜合法的一般步驟是:一作二說三求。②向量法,運用向量法求二面角應注意的是計算。很多同學都會應用向量法求二面角,但結果往往求不對,出現的問題就是計算錯誤。


 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案 藍天教育暑假優化學習系列答案
藍天教育暑假優化學習系列答案科目:高中數學 來源: 題型:解答題
如圖甲,設正方形 的邊長為
的邊長為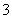 ,點
,點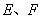 分別在
分別在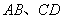 上,并且滿足
上,并且滿足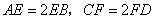 ,如圖乙,將直角梯形
,如圖乙,將直角梯形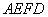 沿
沿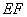 折到
折到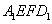 的位置,使點
的位置,使點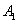 在
在
平面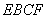 上的射影
上的射影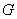 恰好在
恰好在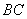 上.
上.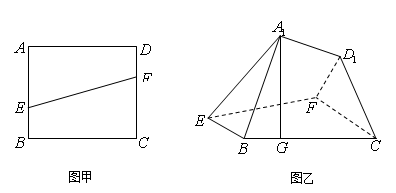
(1)證明: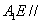 平面
平面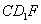 ;
;
(2)求平面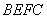 與平面
與平面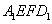 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
AB為圓O的直徑,點E、F在圓上,AB//EF,矩形ABCD所在平面與圓O所在平面互相垂直,已知AB=2,BC=EF=1。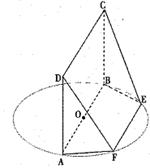
(I)求證:BF⊥平面DAF;
(II)求ABCD與平面CDEF所成銳二面角的某三角函數值;
(III)求多面體ABCDFE的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知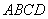 為平行四邊形,
為平行四邊形,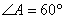 ,
,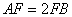 ,
,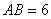 ,點
,點 在
在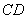 上,
上,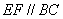 ,
,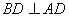 ,
,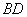 與
與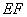 相交于
相交于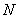 .現將四邊形
.現將四邊形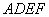 沿
沿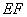 折起,使點
折起,使點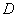 在平面
在平面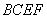 上的射影恰在直線
上的射影恰在直線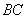 上.
上.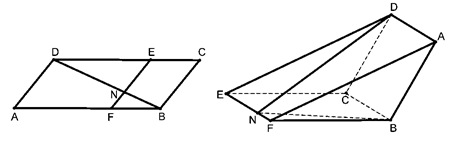
(Ⅰ) 求證: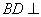 平面
平面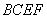 ;
;
(Ⅱ) 求折后直線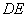 與平面
與平面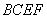 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,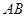 為圓
為圓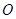 的直徑,點
的直徑,點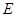 、
、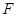 在圓
在圓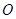 上,
上,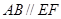 ,矩形
,矩形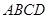 所在的平面與圓
所在的平面與圓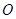 所在的平面互相垂直.已知
所在的平面互相垂直.已知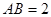 ,
,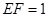 .
.
(Ⅰ)求證:平面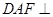 平面
平面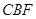 ;
;
(Ⅱ)求直線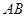 與平面
與平面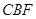 所成角的大小;
所成角的大小;
(Ⅲ)當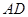 的長為何值時,平面
的長為何值時,平面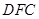 與平面
與平面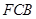 所成的銳二面角的大小為
所成的銳二面角的大小為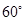 ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
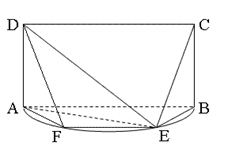
如圖,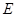 是以
是以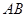 為直徑的半圓上異于
為直徑的半圓上異于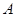 、
、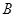 的點,矩形
的點,矩形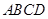 所在的平面垂直于該半圓所在的平面,且
所在的平面垂直于該半圓所在的平面,且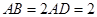 .
.
(Ⅰ)求證: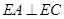 ;
;
(Ⅱ)設平面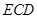 與半圓弧的另一個交點為
與半圓弧的另一個交點為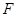 .
.
①試證: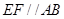 ;
;
②若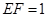 ,求三棱錐
,求三棱錐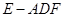 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱錐 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分別是AP、AD的中點.
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分別是AP、AD的中點.
求證:(1)直線EF∥平面PCD;
(2)平面BEF⊥平面PAD
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com