
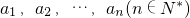 ,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”.
,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”.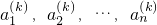 ,k=1,2,….
,k=1,2,….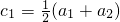 ,則
,則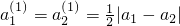 ,即經T1(c1)后,前兩項相等;
,即經T1(c1)后,前兩項相等;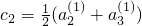 ,則
,則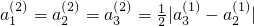 ,即經T2(c2)后,前3項相等;
,即經T2(c2)后,前3項相等;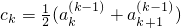 ,變換后數列變為
,變換后數列變為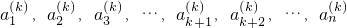 ,則
,則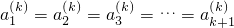 ;
;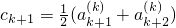 ,
,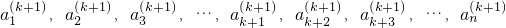 ,
,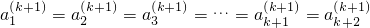 ;
;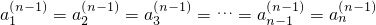 ;
;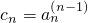 ,經過變換Tn(cn)后,數列各項均為0.
,經過變換Tn(cn)后,數列各項均為0.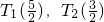 )
)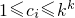 ,i=1,2,…,k.
,i=1,2,…,k.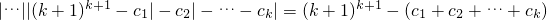 ≥(k+1)k+1-k•kk>0
≥(k+1)k+1-k•kk>0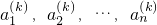 .取
.取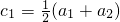 ,
,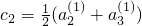 ,繼續做類似的變換,取
,繼續做類似的變換,取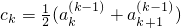 ,(k≤n-1),經Tk(ck)后,得到數列的前k+1項相等,再取
,(k≤n-1),經Tk(ck)后,得到數列的前k+1項相等,再取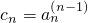 ,經Tn(cn)后,即可得到結論;
,經Tn(cn)后,即可得到結論;

 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2012-2013學年北京市朝陽區高三(上)期中數學試卷(理科)(解析版) 題型:解答題
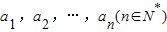 ,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”.
,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”.查看答案和解析>>
科目:高中數學 來源:2012-2013學年北京市朝陽區高三(上)期中數學試卷(理科)(解析版) 題型:解答題
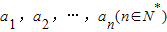 ,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”.
,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”.查看答案和解析>>
科目:高中數學 來源:2012-2013學年北京市朝陽區高三(上)期中數學試卷(文科)(解析版) 題型:解答題
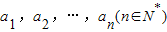 ,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”
,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1-c|,|a2-c|,…,|an-c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com