
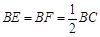 ,將△AED、△CFD分別沿DE、DF折起,使A、C兩點重合于點
,將△AED、△CFD分別沿DE、DF折起,使A、C兩點重合于點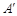 ,連結A¢B.
,連結A¢B.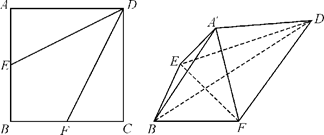
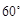 .
.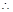 直線EF與A¢D的位置關系是異面垂直 4分
直線EF與A¢D的位置關系是異面垂直 4分
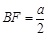 ,A¢E=A¢F=
,A¢E=A¢F= ,EF=
,EF= ,則
,則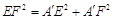 ,
,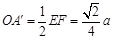 ,
,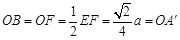 ,
, ,∴
,∴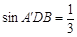 ,
,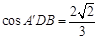 ,
,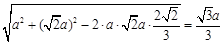 ,所以
,所以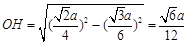 ,
,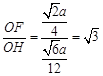 ,故ÐOHF=
,故ÐOHF=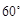 .
.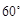 . 12分
. 12分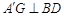 于G,可得A¢G⊥面BEDF,
于G,可得A¢G⊥面BEDF,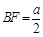 ,A¢E=A¢F=
,A¢E=A¢F= ,EF=
,EF= ,則
,則 ,
,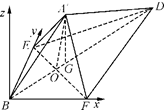
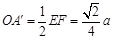 ,
,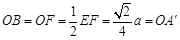 ,則
,則 ,
,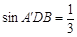 ,
,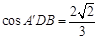 ,
,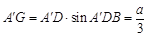 ,
,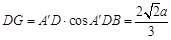 ,則
,則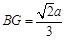 ,
, 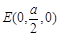 ,
,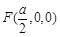 ,
, 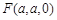 ,
,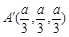 ,故
,故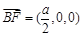 ,
, ,
,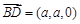 ,
, ,
, ,
,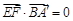 ,故面A¢BD的一個法向量
,故面A¢BD的一個法向量 ,
,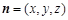 ,則
,則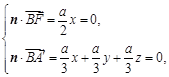 取
取 ,
,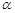 ,則
,則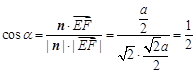 ,∴
,∴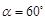 ,
,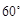 . 12分
. 12分

科目:高中數學 來源:不詳 題型:解答題
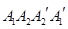 ,滿足
,滿足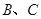 在
在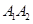 上,
上,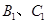 在
在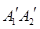 上,且
上,且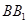 ∥
∥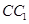 ∥
∥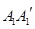 ,
,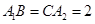 ,
,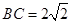 ,
,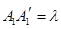 ,沿
,沿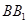 、
、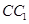 將矩形
將矩形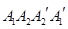 折起成為一個直三棱柱,使
折起成為一個直三棱柱,使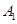 與
與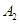 、
、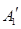 與
與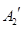 重合后分別記為
重合后分別記為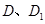 ,在直三棱柱
,在直三棱柱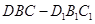 中,點
中,點 分別為
分別為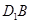 和
和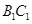 的中點.
的中點.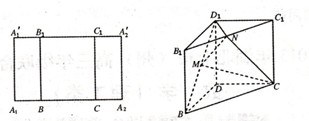
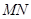 ∥平面
∥平面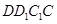 ;
;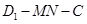 為直二面角,求
為直二面角,求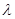 的值.
的值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 =
= =90°
=90° =1200,AD=AB=1,AC交BD于 O 點.
=1200,AD=AB=1,AC交BD于 O 點.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 平面EFDC,設AD中點為P.
平面EFDC,設AD中點為P.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
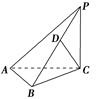
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com