
【題目】設函數f(x)=ax2+bx+c(a,b,c∈R),若x=﹣1為函數y=f(x)ex的一個極值點,則下列圖象不可能為y=f(x)的圖象是( )
A. 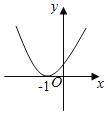 B.
B. 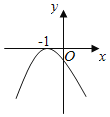
C. 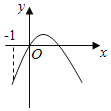 D.
D. 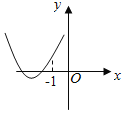
【答案】D
【解析】
先求出函數f(x)ex的導函數,利用x=﹣1為函數f(x)ex的一個極值點可得a,b,c之間的關系,再代入函數f(x)=ax2+bx+c,對答案分別代入驗證,看哪個答案不成立即可.
解:由y=f(x)ex=ex(ax2+bx+c)y′=f′(x)ex+exf(x)=ex[ax2+(b+2a)x+b+c],
由x=﹣1為函數f(x)ex的一個極值點可得,﹣1是方程ax2+(b+2a)x+b+c=0的一個根,
所以有a﹣(b+2a)+b+c=0c=a.
法一:所以函數f(x)=ax2+bx+a,對稱軸為x![]() ,且f(﹣1)=2a﹣b,f(0)=a.
,且f(﹣1)=2a﹣b,f(0)=a.
對于A,由圖得a>0,f(0)>0,f(﹣1)=0,不矛盾,
對于B,由圖得a<0,f(0)<0,f(﹣1)=0,不矛盾,
對于C,由圖得a<0,f(0)<0,x![]() 0b>0f(﹣1)<0,不矛盾,
0b>0f(﹣1)<0,不矛盾,
對于D,由圖得a>0,f(0)>0,x![]() 1b>2af(﹣1)<0與原圖中f(﹣1)>0矛盾,D不對.
1b>2af(﹣1)<0與原圖中f(﹣1)>0矛盾,D不對.
法二:所以函數f(x)=ax2+bx+a,由此得函數相應方程的兩根之積為1,對照四個選項發現,D不成立.
故選:D.


科目:高中數學 來源: 題型:
【題目】高三一班、二班各有6名學生去參加學校組織的高中數學競賽選拔考試,成績如莖葉圖所示.
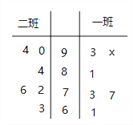
(1)若一班、二班6名學生的平均分相同,求![]() 值;
值;
(2)若將競賽成績在![]() 、
、![]() 、
、![]() 內的學生在學校推優時,分別賦分、2分、3分,現在從一班的6名參賽學生中選兩名,求推優時,這兩名學生賦分的和為4分的概率.
內的學生在學校推優時,分別賦分、2分、3分,現在從一班的6名參賽學生中選兩名,求推優時,這兩名學生賦分的和為4分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義域為![]() 的函數
的函數![]() 滿足:對于任意的實數
滿足:對于任意的實數![]() 都有
都有![]() 成立,且當
成立,且當![]() 時,
時,![]() .
.
(Ⅰ)判斷函數![]() 的奇偶性,并證明你的結論;
的奇偶性,并證明你的結論;
(Ⅱ)證明![]() 在
在![]() 上為減函數;
上為減函數;
(Ⅲ)若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 、
、![]() 的坐標分別是
的坐標分別是![]() ,
,![]() ,直線
,直線![]() ,
,![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() .
.
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)若過點![]() 的直線
的直線![]() 交動點
交動點![]() 的軌跡于
的軌跡于![]() 、
、![]() 兩點, 且
兩點, 且![]() 為線段
為線段![]() ,
,![]() 的中點,求直線
的中點,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)是定義在R上的奇函數,且當x≥0時,f(x)=-x2+ax.
(1)若a=-2,求函數f(x)的解析式;
(2)若函數f(x)為R上的單調減函數,
①求a的取值范圍;
②若對任意實數m,f(m-1)+f(m2+t)<0恒成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. “f(0)![]() ”是“函數f(x)是奇函數”的充要條件
”是“函數f(x)是奇函數”的充要條件
B. 若p:![]() ,
,![]() ,則
,則![]() :
:![]() ,
,![]()
C. “若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”
”
D. 若![]() 為假命題,則p,q均為假命題
為假命題,則p,q均為假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=b·ax(其中a,b為常量,且a>0,a≠1)的圖象經過點A(1,6),B(3,24).
(1)求f(x);
(2)若不等式(![]() )x+(
)x+(![]() )x-m≥0在x∈(-∞,1]時恒成立,求實數m的取值范圍.
)x-m≥0在x∈(-∞,1]時恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com