
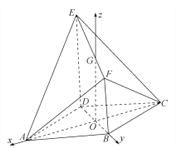
【題目】如圖所示的幾何體![]() 中,底面
中,底面![]() 為菱形,
為菱形, ![]() ,
, ![]() ,
, ![]() 與
與![]() 相交于
相交于![]() 點,四邊形
點,四邊形![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.
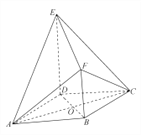
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:
(1)利用題意證得![]() 平面
平面![]() .由面面垂直的判斷定理可得平面
.由面面垂直的判斷定理可得平面![]() 平面
平面![]() .
.
(2)結合(1)的結論和題意建立空間直角坐標系,由平面的法向量可得二面角![]() 的余弦值為
的余弦值為![]() .
.
試題解析:
(1)因為底面![]() 為菱形,所以
為菱形,所以![]() ,
,
又平面![]() 底面
底面![]() ,平面
,平面![]() 平面
平面![]() ,
,
因此![]() 平面
平面![]() ,從而
,從而![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
由![]() ,
, ![]() ,
, ![]() ,
,
可知![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
從而![]() ,故
,故![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)取![]() 中點
中點![]() ,由題可知
,由題可知![]() ,所以
,所以![]() 平面
平面![]() ,又在菱形
,又在菱形![]() 中,
中, ![]() ,所以分別以
,所以分別以![]() ,
, ![]() ,
, ![]() 的方向為
的方向為![]() ,
, ![]() ,
, ![]() 軸正方向建立空間直角坐標系
軸正方向建立空間直角坐標系![]() (如圖示),
(如圖示),
則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() .
.
由(1)可知![]() 平面
平面![]() ,所以平面
,所以平面![]() 的法向量可取為
的法向量可取為![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
則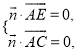 即
即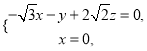 即
即 令
令![]() ,得
,得![]() ,
,
所以![]() .
.
從而![]()
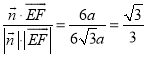 .
.
故所求的二面角![]() 的余弦值為
的余弦值為![]() .
.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁四位同學中僅有一人申請了北京大學的自主招生考試,當他們被問到誰申請了北京大學的自主招生考試時,甲說:“丙或丁申請了”;乙說:“丙申請了”;丙說:“甲和丁都沒有申請”;丁說:“乙申請了”,如果這四位同學中只有兩人說的是對的,那么申請了北京大學的自主招生考試的同學是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學擬在高一下學期開設游泳選修課,為了了解高一學生喜歡游泳是否與性別有關,現從高一學生中抽取100人做調查,得到![]() 列聯表,且已知在100個人中隨機抽取1人,抽到喜歡游泳的學生的概率為
列聯表,且已知在100個人中隨機抽取1人,抽到喜歡游泳的學生的概率為![]() .
.
(1)請完成![]() 列聯表;
列聯表;
喜歡游泳 | 不喜歡游泳 | 合計 | |
男生 | 40 | ||
女生 | 30 | ||
合計 | 100 |
(2)根據列聯表,是否有99.9%的把握認為喜歡游泳與性別有關?并說明你的理由.
附:參考公式與臨界值表如下:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
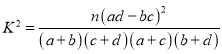
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的左焦點為
的左焦點為![]() ,且點
,且點![]() 在C上.
在C上.
![]() 求C的方程;
求C的方程;
![]() 設點P關于x軸的對稱點為點
設點P關于x軸的對稱點為點![]() 不經過P點且斜率為k的直線l與C交于A,B兩點,直線PA,PB分別與x軸交于點M,N,若
不經過P點且斜率為k的直線l與C交于A,B兩點,直線PA,PB分別與x軸交于點M,N,若![]() ,求k.
,求k.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() :
: ![]() (
(![]() 為參數,
為參數, ![]() ),在以坐標原點為極點,
),在以坐標原點為極點, ![]() 軸的非負半軸為極軸的極坐標系中,曲線
軸的非負半軸為極軸的極坐標系中,曲線![]() :
: ![]() .
.
(1)試將曲線![]() 與
與![]() 化為直角坐標系
化為直角坐標系![]() 中的普通方程,并指出兩曲線有公共點時
中的普通方程,并指出兩曲線有公共點時![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,兩曲線相交于
時,兩曲線相交于![]() ,
, ![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線![]() ,直線l的參數方程為:
,直線l的參數方程為:![]() (
(![]() 為參數),直線l與曲線C分別交于M,N兩點.
為參數),直線l與曲線C分別交于M,N兩點.
(1)寫出曲線C的直角坐標方程和直線l的普通方程;
(2)若點![]() ,求
,求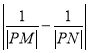 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面上有7個點,每三點的兩兩連線都組成一個不等邊三角形.求證:一定可以找到4對三角形,使每對三角形的公共邊既是其中一個三角形的最長邊又是另一個三角形的最短邊.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com