
【題目】已知線段AB的端點B的坐標為(3,0),端點A在圓![]() 上運動;
上運動;
(1)求線段AB中點M的軌跡方程;
(2)過點C(1,1)的直線m與M的軌跡交于G、H兩點,當△GOH(O為坐標原點)的面積最大時,求直線m的方程并求出△GOH面積的最大值.
(3)若點C(1,1),且P在M軌跡上運動,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)設出A,M坐標,利用M為線段AB中點,確定A,M坐標之間的關系,根據點A在圓![]() 上運動,可得線段AB中點M的軌跡方程;(2)令
上運動,可得線段AB中點M的軌跡方程;(2)令![]() ,則
,則![]() ,即
,即![]() 時
時![]() 面積最大為2,從而得到直線m的方程;(3)設點
面積最大為2,從而得到直線m的方程;(3)設點![]() ,則
,則![]() ,令
,令![]() ,由直線與圓的位置關系得到
,由直線與圓的位置關系得到![]() 的取值范圍.
的取值范圍.
(1)解:設點![]()
由中點坐標公式有
又點![]() 在圓
在圓![]() 上,將
上,將![]() 點坐標代入圓方程得:
點坐標代入圓方程得:
![]() 點的軌跡方程為:
點的軌跡方程為:![]()
(2)令![]() ,則
,則![]()
當![]() ,即
,即![]() 時
時![]() 面積最大為2
面積最大為2
又直線![]() 過點
過點![]() ,
,![]() ,∴
,∴![]() 到直線
到直線![]() 的距離為
的距離為![]() ,當直線
,當直線![]() 斜率不存在時
斜率不存在時![]() ,
,![]() 到
到![]() 的距離為1不滿足,令
的距離為1不滿足,令![]()
故直線![]() 的方程為:
的方程為:![]()
(3)設點![]() ,由于點
,由于點![]()
則![]() ,令
,令![]()
有![]() ,由于點
,由于點![]() 在圓
在圓![]() 上運動,故滿足圓的方程.
上運動,故滿足圓的方程.
當直線![]() 與圓相切時,
與圓相切時,![]() 取得最大或最小
取得最大或最小
故有![]()
所以![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓心在![]() 軸上的圓
軸上的圓![]() 經過兩點
經過兩點![]() 和
和![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)當![]() 時,
時,![]() 為直線
為直線![]() 上的定點,若圓
上的定點,若圓![]() 上存在唯一一點
上存在唯一一點![]() 滿足
滿足![]() ,求定點
,求定點![]() 的坐標;
的坐標;
(3)設點A,B為圓![]() 上任意兩個不同的點,若以AB為直徑的圓與直線
上任意兩個不同的點,若以AB為直徑的圓與直線![]() 都沒有公共點,求實數
都沒有公共點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在對人們的休閑方式的一次調查中,用簡單隨機抽樣方法調查了125人,其中女性70人,男性55人.女性中有40人主要的休閑方式是看電視,另外30人主要的休閑方式是運動;男性中有20人主要的休閑方式是看電視,另外35人主要的休閑方式是運動.
(1)根據以上數據建立一個![]() 列聯表;
列聯表;
(2)能否在犯錯誤的概率不超過0.025的前提下,認為性別與休閑方式有關系?
(3)在休閑方式為看電視的人中按分層抽樣方法抽取6人參加某機構組織的健康講座,講座結束后再從這6人中抽取2人作反饋交流,求參加交流的恰好為2位女性的概率.
附:
P( | 0.05 | 0.025 | 0.010 |
k | 3.841 | 5.024 | 6.635 |
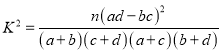
休閑方式 性別 | 看電視 | 運動 | 合計 |
女 | |||
男 | |||
合計 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某區“創文明城區”(簡稱“創城”)活動中,教委對本區![]() 四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
學校 |
|
|
|
|
抽查人數 | 50 | 15 | 10 | 25 |
“創城”活動中參與的人數 | 40 | 10 | 9 | 15 |
(注:參與率是指:一所學校“創城”活動中參與的人數與被抽查人數的比值)假設每名高中學生是否參與”創城”活動是相互獨立的.
(1)若該區共2000名高中學生,估計![]() 學校參與“創城”活動的人數;
學校參與“創城”活動的人數;
(2)在隨機抽查的100名高中學生中,隨機抽取1名學生,求恰好該生沒有參與“創城”活動的概率;
(3)在上表中從![]() 兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好
兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好![]() 兩校各有1人沒有參與“創城”活動的概率是多少?
兩校各有1人沒有參與“創城”活動的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
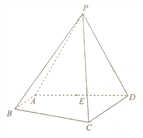
【題目】如圖,在四棱錐![]() 中,
中, ![]() 是等邊三角形,
是等邊三角形, ![]() 為
為![]() 的中點,四邊形
的中點,四邊形![]() 為直角梯形,
為直角梯形, ![]()
![]()
![]()
![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求四棱錐![]() 的體積;
的體積;
(3)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設正項數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足:
,且滿足:![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求數列![]() 的通項公式;
的通項公式;
(Ⅱ)若正項等比數列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,若對任意
,若對任意![]() ,均有
,均有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有如下命題:
有如下命題:
①![]() ; ②函數的圖象關于原點中心對稱;
; ②函數的圖象關于原點中心對稱;
③函數的定義域與值域相同; ④函數的圖象必經過第二、四象限.
其中正確命題的個數是( )
A.4B.3C.2D.1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com