
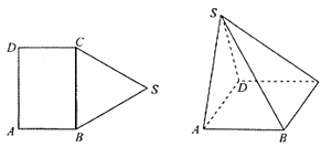
【題目】如圖,五邊形![]() 中,四邊形
中,四邊形![]() 為長方形,
為長方形,![]() 為邊長為
為邊長為![]() 的正三角形,將
的正三角形,將![]() 沿
沿![]() 折起,使得點
折起,使得點![]() 在平面
在平面![]() 上的射影恰好在
上的射影恰好在![]() 上.
上.
(Ⅰ)當![]() 時,證明:平面
時,證明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成二面角的余弦值的絕對值.
所成二面角的余弦值的絕對值.
【答案】(Ⅰ)證明見解析;(Ⅱ)![]() .
.
【解析】
試題
(Ⅰ)作![]() ,垂足為
,垂足為![]() ,依題意得
,依題意得![]() 平面
平面![]() ,則
,則![]() ,
,![]() 平面
平面![]() ,
,![]() ,結合勾股定理可得
,結合勾股定理可得![]() ,則
,則![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
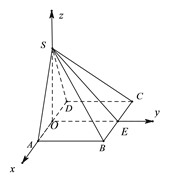
(Ⅱ)由幾何關系,以![]() 為
為![]() 軸建立空間直角坐標系,由題意可得平面
軸建立空間直角坐標系,由題意可得平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() .計算可得平面
.計算可得平面![]() 與平面
與平面![]() 所成二面角的余弦值的絕對值為
所成二面角的余弦值的絕對值為![]() .
.
試題解析:
(Ⅰ)作![]() ,垂足為
,垂足為![]() ,依題意得
,依題意得![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]()
利用勾股定理得![]() ,同理可得
,同理可得![]() .
.
在![]() 中,
中,![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]()
(Ⅱ)連結![]() ,
,![]() ,
,![]() ,
,
![]() ,又四邊形
,又四邊形![]() 為長方形,
為長方形,![]() .
.
取![]() 中點為
中點為![]() ,得
,得![]() ∥
∥![]() ,連結
,連結![]() ,
,
其中![]() ,
,![]() ,
,![]()
由以上證明可知![]() 互相垂直,不妨以
互相垂直,不妨以![]() 為
為![]() 軸建立空間直角坐標系.
軸建立空間直角坐標系.![]() ,
,
![]() ,
,
設![]() 是平面
是平面![]() 的法向量,
的法向量,
則有 即
即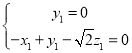 ,
,
令![]() 得
得![]()
設![]() 是平面
是平面![]() 的法向量,
的法向量,
則有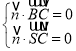 即
即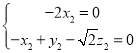
令![]() 得
得![]() .
.
則
所以平面![]() 與平面
與平面![]() 所成二面角的余弦值的絕對值為
所成二面角的余弦值的絕對值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某班要從6名男生4名女生中選出5人擔任5門不同學科的課代表,請分別求出滿足下列條件的方法種數![]() 結果用數字作答
結果用數字作答![]() .
.
(1)所安排的男生人數不少于女生人數;
(2)男生甲必須是課代表,但不能擔任語文課代表;
(3)女生乙必須擔任數學課代表,且男生甲必須擔任課代表,但不能擔任語文課代表.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,過拋物線C:y2=2px(p>0)的準線l上的點M(﹣1,0)的直線l1交拋物線C于A,B兩點,線段AB的中點為P.
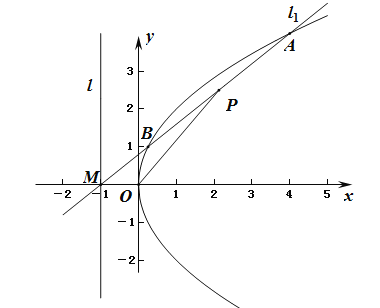
(Ⅰ)求拋物線C的方程;
(Ⅱ)若|MA||MB|=λ|OP|2,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 已知函數f(x)=|x+a|+|x-2|.
(1)當a=-3時,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 與斜率為
與斜率為![]() 且過拋物線焦點
且過拋物線焦點![]() 的直線
的直線![]() 交于
交于![]() 、
、![]() 兩點,滿足弦長
兩點,滿足弦長![]() .
.
(1)求拋物線的標準方程;
(2)已知![]() 為拋物線上任意一點,
為拋物線上任意一點,![]() 為拋物線內一點,求
為拋物線內一點,求![]() 的最小值,以及此時點
的最小值,以及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓C的參數方程為![]() (θ為參數),直線l經過點P(1,2),傾斜角α=
(θ為參數),直線l經過點P(1,2),傾斜角α=![]() .
.
(1)寫出圓C的普通方程和直線l的參數方程;
(2)設直線l與圓C相交于A,B兩點,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為直角梯形,
中,底面ABCD為直角梯形,![]()
![]() ,
,![]() 平面ABCD,E是棱PC上的一點.
平面ABCD,E是棱PC上的一點.
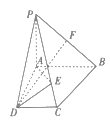
(1)證明:平面![]() 平面
平面![]() .
.
(2)若![]() ,F是PB的中點,
,F是PB的中點,![]() ,
,![]() ,求直線DF與平面
,求直線DF與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com