
(Ⅰ)求雙曲線C的方程;
(Ⅱ)過點P(0,4)的直線l,交雙曲線C于A、B兩點,交x軸于Q點(Q點與C的頂點不重合).當![]() =λ1
=λ1![]() =λ2
=λ2![]() ,且λ1+λ2=-
,且λ1+λ2=-![]() 時,求Q點的坐標.
時,求Q點的坐標.
解:(Ⅰ)設雙曲線方程為![]() -
-![]() =1.
=1.
由橢圓![]() +
+![]() =1求得兩焦點為(-2,0),(2,0).
=1求得兩焦點為(-2,0),(2,0).
∴對于雙曲線C:c=2,又y=![]() x為雙曲線C的一條漸近線,
x為雙曲線C的一條漸近線,
∴![]() =
=![]() 解得a2=1,b2=3,∴雙曲線C的方程為:x2-
解得a2=1,b2=3,∴雙曲線C的方程為:x2-![]() =1.
=1.
(Ⅱ)解法一:由題意知直線l的斜率k存在且不等于零.
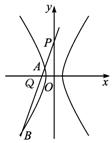
設l的方程:y=kx+4,A(x1,y1),B(x2,y2),
則Q(-![]() ,0),
,0),
∵![]() =λ1
=λ1![]() ,
,
∴(-![]() ,-4)=λ1(x1+
,-4)=λ1(x1+![]() ,y1).
,y1).
∴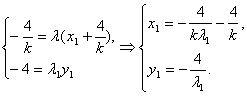
∵A(x1,y1)在雙曲線C上,∴![]() -
-![]() -1=0,
-1=0,
∴16+32λ1+16![]() -
-![]() k2-k2
k2-k2![]() =0,
=0,
∴(16-k2)![]() +32λ1+16-
+32λ1+16-![]() k2=0,
k2=0,
同理有:(16-k2)λ22+32λ2+16-![]() k2=0,
k2=0,
若16-k2=0,則直線l過頂點,不合題意,∴16-k2≠0,
∴λ1、λ2是二次方程(16-k2)x2+32x+16-![]() k2=0的兩根,
k2=0的兩根,
∴λ1+λ2=![]() =-
=-![]() ,∴k2=4,此時Δ>0,∴k=±2.
,∴k2=4,此時Δ>0,∴k=±2.
∴所求Q點坐標為(±2,0).
解法二:由題意知直線l的斜率k存在且不等于0,設l的方程為:
y=kx+4,A(x1,y1),B(x2,y2,)則Q(-![]() ,0),∵
,0),∵![]() =λ1
=λ1![]() ,
,
∴Q分![]() 的比為λ1,由定比分點坐標公式得
的比為λ1,由定比分點坐標公式得
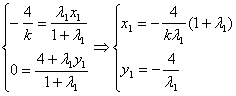 下同解法一
下同解法一
解法三:由題意知直線l的斜率k存在且不等于0.
設l的方程:y=kx+4,A(x1,y1),B(x2,y2),則Q(-![]() ,0),∵
,0),∵![]() =λ1
=λ1![]() =λ2
=λ2![]() ,∴(-
,∴(-![]() ,-4)=λ1(x1+
,-4)=λ1(x1+![]() ,y1)=λ2(x+
,y1)=λ2(x+![]() ,y2),
,y2),
∴-4=λ1y1=λ2y2,λ1=-![]() ,λ2=-
,λ2=-![]() ,又λ1+λ2=-
,又λ1+λ2=-![]() ,
,
∴![]() =
=![]() .
.
即3(y1+y2)=2y1y2.
將y=kx+4代入x2-![]() =1得
=1得
(3-k2)y2-24y+48-3k2=0.
∵3-k2≠0,否則l與漸近線平行,
∴y1+y2=![]() ,y1y2=
,y1y2=![]() .
.
∴3×![]() =2×
=2×![]() .
.
∴k=±2.
∴Q(±2,0).
解法四:
由題意知直線l的斜率k存在且不等于零
設l的方程:y=kx+4,A(x1,y1),B(x2,y2,)則Q(-![]() ,0).
,0).
∵![]() =λ1
=λ1![]() ,
,
∴(-![]() ,-4)=λ1(x1+
,-4)=λ1(x1+![]() ,y1).
,y1).
∴λ1=![]() =-
=-![]() .
.
同理 λ2=-![]() .
.
λ1+λ2=-![]() -
-![]() =-
=-![]() .
.
即2k2x1x2+5k(x1+x2)+8=0. (*)
又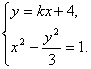
消去y得
(3-k2)x2-8kx-19=0.
當3-k2=0時,則直線l與雙曲線的漸近線平行,不合題意,3-k2≠0.
由韋達定理有:
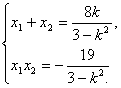
代入(*)式得k2=4,k=±2
∴所求Q點的坐標為(±2,0).


科目:高中數學 來源: 題型:
| x2 |
| 8 |
| y2 |
| 4 |
| ||
| 3 |
| MP |
| MQ |
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)求雙曲線C的方程;
(2)過點P(0,4)的直線l,交雙曲線C于A、B兩點,交x軸于Q點(Q點與C的頂點不重合).當![]() =λ1
=λ1![]() =λ2
=λ2![]() ,且λ1+λ2=-
,且λ1+λ2=-![]() 時,求Q點的坐標.
時,求Q點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
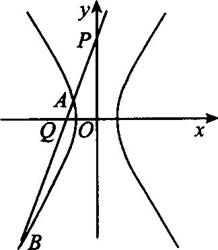
第20題圖
(1)求雙曲線C的方程;
(2)過點p(0,4)的直線l交雙曲線C于A、B兩點,交x軸于Q點(Q點與C的頂點不重合),當![]() =λ1
=λ1![]() =λ2
=λ2![]() ,且λ1+λ2=時,求Q點的坐標.
,且λ1+λ2=時,求Q點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com