
兩點等分單位圓時,有相應正確關系為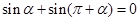 ;三點等分單位圓時,有相應正確關系為
;三點等分單位圓時,有相應正確關系為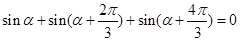 。由此可以推知:四點等分單位圓時的相應正確關系為
。由此可以推知:四點等分單位圓時的相應正確關系為

【解析】
試題分析:用兩點等分單位圓時,關系為sinα+sin(π+α)=0,兩個角的正弦值之和為0,且第一個角為α,第二個角與第一個角的差為:(π+α)-α=π,
用三點等分單位圓時,關系為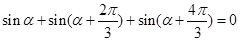 ,此時三個角的正弦值之和為0,且第一個角為α,第二個角與第一個角的差與第三個角與第二個角的差相等,均為有(
,此時三個角的正弦值之和為0,且第一個角為α,第二個角與第一個角的差與第三個角與第二個角的差相等,均為有(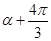 )-(
)-(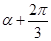 )=(
)=(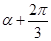 )-α=
)-α=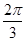 .
.
依此類推,可得當四點等分單位圓時,為四個角正弦值之和為0,且第一個角為α,第二個角為
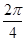 +α=
+α=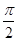 +α,第三個角
+α,第三個角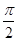 +α+
+α+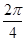 =π+α,第四個角為π+α+
=π+α,第四個角為π+α+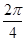 =
=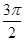 +α,
+α,
即其關系為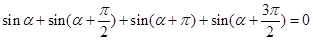 。
。
考點:本題主要考查歸納推理。
點評:中檔題,解題的關鍵在于分析兩點等分單位圓與三點等分單位圓的正弦值的個數(shù)及角的關系,歸納得出關系式變化的規(guī)律。


科目:高中數(shù)學 來源: 題型:
| 2π |
| 3 |
| 4π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
運用物理中矢量運算及向量坐標表示與運算,我們知道:
(1)若兩點等分單位圓時,有相應關系為:![]() (2)四點等分單位圓時,有相應關系為:
(2)四點等分單位圓時,有相應關系為:
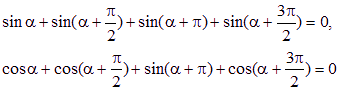
由此可以推知三等分單位圓時的相應關系為:
查看答案和解析>>
科目:高中數(shù)學 來源:2014屆湖北穩(wěn)派教育高三10月聯(lián)合調研考試理科數(shù)學試卷(解析版) 題型:填空題
運用物理中矢量運算及向量坐標表示與運算,我們知道:兩點等分單位圓時,有相應正確關系為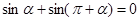 ,三等分單位圓時,有相應正確關系為
,三等分單位圓時,有相應正確關系為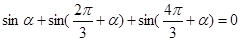 ,由此推出:四等分單位圓時的相應正確關系為
.
,由此推出:四等分單位圓時的相應正確關系為
.
查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年江西省高三第四次月考理科數(shù)學試卷 題型:填空題
兩點等分單位圓時,有相應正確關系為: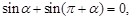 三點等分單位圓時,有相應正確關系為:
三點等分單位圓時,有相應正確關系為: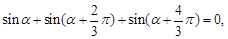 由此可以推知四點等分單位圓時的相應正確關系為__________
由此可以推知四點等分單位圓時的相應正確關系為__________
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年江西省高三上學期期中考試數(shù)學理卷 題型:填空題
兩點等分單位圓時,有相應正確關系為: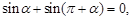 三點等分單位圓時,有相應正確關系為:
三點等分單位圓時,有相應正確關系為: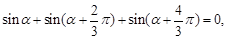 由此可以推知四點等分單位圓時的相應正確關系為
.
由此可以推知四點等分單位圓時的相應正確關系為
.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com