
【題目】已知函數![]() .
.
(1)若曲線![]() 在點
在點![]() 處的切線
處的切線![]() 與直線
與直線![]() 垂直,求實數
垂直,求實數![]() 的值;
的值;
(2)若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)證明:![]()
科目:高中數學 來源: 題型:
【題目】已知函數![]() 定義域為
定義域為![]() ,設
,設![]() .
.
(1)試確定![]() 的取值范圍,使得函數
的取值范圍,使得函數![]() 在
在![]() 上為單調函數;
上為單調函數;
(2)求證:![]() ;
;
(3)求證:對于任意的![]() ,總存在
,總存在![]() ,滿足
,滿足![]() ,并確定這樣的
,并確定這樣的![]() 的個數.
的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在全面抗擊新冠肺炎疫情這一特殊時期,我市教育局提出“停課不停學”的口號,鼓勵學生線上學習.某校數學教師為了調查高三學生數學成績與線上學習時間之間的相關關系,對高三年級隨機選取45名學生進行跟蹤問卷,其中每周線上學習數學時間不少于5小時的有19人,余下的人中,在檢測考試中數學平均成績不足120分的占![]() ,統計成績后得到如下
,統計成績后得到如下![]() 列聯表:
列聯表:
分數不少于120分 | 分數不足120分 | 合計 | |
線上學習時間不少于5小時 | 4 | 19 | |
線上學習時間不足5小時 | |||
合計 | 45 |
(1)請完成上面![]() 列聯表;并判斷是否有99%的把握認為“高三學生的數學成績與學生線上學習時間有關”;
列聯表;并判斷是否有99%的把握認為“高三學生的數學成績與學生線上學習時間有關”;
(2)在上述樣本中從分數不少于120分的學生中,按照分層抽樣的方法,抽到線上學習時間不少于5小時和線上學習時間不足5小時的學生共5名,若在這5名學生中隨機抽取2人,求至少1人每周線上學習時間不足5小時的概率.
(下面的臨界值表供參考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式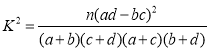 其中
其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果函數![]() 的導函數
的導函數![]() 的圖象如圖所示,則以下關于函數
的圖象如圖所示,則以下關于函數![]() 的判斷:
的判斷:
①在區間![]() 內單調遞增;
內單調遞增;
②在區間![]() 內單調遞減;
內單調遞減;
③在區間![]() 內單調遞增;
內單調遞增;
④![]() 是極小值點;
是極小值點;
⑤![]() 是極大值點.
是極大值點.
其中正確的是( )
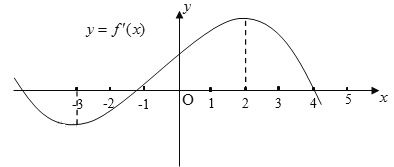
A. ③⑤B. ②③C. ①④⑤D. ①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】3月3日,武漢大學人民醫院的團隊在預印本平臺![]() 上發布了一項研究:在新冠肺炎病例的統計數據中,男性患者往往比女性患者多.研究者分析了1月1日~29日的6013份病例數據,發現
上發布了一項研究:在新冠肺炎病例的統計數據中,男性患者往往比女性患者多.研究者分析了1月1日~29日的6013份病例數據,發現![]() 的患者為男性;進入重癥監護病房的患者中,則有
的患者為男性;進入重癥監護病房的患者中,則有![]() 為男性.隨后,他們分析了武漢大學人民醫院的數據.他們按照癥狀程度的不同進行分析,結果發現,男性患者有
為男性.隨后,他們分析了武漢大學人民醫院的數據.他們按照癥狀程度的不同進行分析,結果發現,男性患者有![]() 為危重,而女性患者危重情況的為
為危重,而女性患者危重情況的為![]() .也就是說男性的發病情況似乎普遍更嚴重.研究者總結道:“男性在新冠肺炎的傳播中扮演著重要的角色.”那么,病毒真的偏愛男性嗎?有一個中學生學習小組,在自己封閉的社區進行無接觸抽樣問卷調查,收集到男、女患者各50個數據,統計如下:
.也就是說男性的發病情況似乎普遍更嚴重.研究者總結道:“男性在新冠肺炎的傳播中扮演著重要的角色.”那么,病毒真的偏愛男性嗎?有一個中學生學習小組,在自己封閉的社區進行無接觸抽樣問卷調查,收集到男、女患者各50個數據,統計如下:
輕—中度感染 | 重度(包括危重) | 總計 | |
男性患者 |
|
|
|
女性患者 |
|
|
|
總計 |
|
|
|
(1)求![]() 列聯表中的數據
列聯表中的數據![]() 的值;
的值;
(2)能否有![]() 把握認為,新冠肺炎的感染程度和性別有關?
把握認為,新冠肺炎的感染程度和性別有關?
(3)該學生實驗小組打算從“輕—中度感染”的患者中按男女比例再抽取5人,追蹤某種中藥制劑的效果.然后從這5人中隨機抽取3人進行每日的健康記錄,求至少抽到2名女性患者的概率.
附表及公式:![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的方程為
的方程為![]() ,曲線
,曲線![]() :
:![]() (
(![]() 為參數,
為參數,![]() ),在以原點
),在以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() :
:![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 有公共點,且直線
有公共點,且直線![]() 與曲線
與曲線![]() 的交點
的交點![]() 恰好在曲線
恰好在曲線![]() 與
與![]() 軸圍成的區域(不含邊界)內,求
軸圍成的區域(不含邊界)內,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com