
【題目】已知函數![]() ,
, ![]() (
(![]() 為常數).
為常數).
(1)若函數![]() 與函數
與函數![]() 在
在![]() 處有相同的切線,求實數
處有相同的切線,求實數![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,證明:
,證明: ![]() ;
;
(3)若對任意![]() ,不等式恒
,不等式恒![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]() .
.
【解析】試題分析:(1)由導數幾何意義得![]() ,因此先求導,再代入得:
,因此先求導,再代入得: ![]() ,
, ![]() ,可得結果;(2)構造差函數
,可得結果;(2)構造差函數![]() ,證明不等式轉化為求其最小值小于零,利用導數求其最大值:
,證明不等式轉化為求其最小值小于零,利用導數求其最大值: ![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() ;(3)不等式恒成立問題,一般利用變量分離轉化為對應函數最值問題,也可直接構造差函數,分類討論最值進行求解.
;(3)不等式恒成立問題,一般利用變量分離轉化為對應函數最值問題,也可直接構造差函數,分類討論最值進行求解.
試題解析:(1)![]() ,則
,則![]() 且
且![]() .
.
所以函數![]() 在
在![]() 處的切線方程為:
處的切線方程為: ![]() ,從而
,從而![]() ,即
,即![]() .
.
(2)由題意知:設函數![]() ,則
,則![]() .
.
設![]() ,從而
,從而![]() 對任意
對任意![]() 恒成立,
恒成立,
所以![]() ,即
,即![]() ,因此函數
,因此函數![]() 在
在![]() 上單調遞減,于是
上單調遞減,于是![]() ,所以當
,所以當![]() 時,
時, ![]() 成立.
成立.
(3)設![]() ,從而對任意
,從而對任意![]() ,不等式
,不等式![]() 恒成立.
恒成立. ![]()
當![]() 時,
時, ![]() 恒成立,此時函數
恒成立,此時函數![]() 單調遞增. 于是,不等式
單調遞增. 于是,不等式![]() 對任意
對任意![]() 恒成立,不符合題意。
恒成立,不符合題意。
2)當![]() ,即
,即![]() 恒成立時,
恒成立時, ![]() 單調遞減.
單調遞減.
設![]() ,則
,則![]() ,
, ![]() ,即
,即![]() ,符合題意。
,符合題意。
3)當![]() 時,設
時,設![]() ,則
,則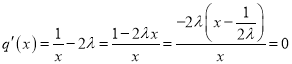
![]() 當
當![]() 時,
時, ![]() ,
, ![]() 單調遞增,
單調遞增,
所以![]() ,故當
,故當![]() 時,函數
時,函數![]() 單調遞增.
單調遞增.
于是當![]() 時,
時, ![]() 成立,不符合題意。
成立,不符合題意。
綜上所述,實數![]() 的取值范圍為
的取值范圍為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】為了對某課題進行討論研究,用分層抽樣的方法從三所高校A、B、C的相關人員中,抽取若干人組成研究小組,有關數據見下表(單位:人)
高校 | 相關人數 | 抽取人數 |
A | x | 1 |
B | 36 | y |
C | 54 | 3 |
(1)求x、y;
(2)若從高校B相關的人中選2人作專題發言,應采用什么抽樣法,請寫出合理的抽樣過程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的單調區間;
(Ⅱ)已知f(x)在x=1處取得極大值.求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
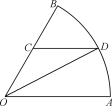
【題目】如圖是一個半徑為2千米,圓心角為![]() 的扇形游覽區的平面示意圖
的扇形游覽區的平面示意圖![]() 是半徑
是半徑![]() 上一點,
上一點,![]() 是圓弧
是圓弧![]() 上一點,且
上一點,且![]() .現在線段
.現在線段![]() ,線段
,線段![]() 及圓弧
及圓弧![]() 三段所示位置設立廣告位,經測算廣告位出租收入是:線段
三段所示位置設立廣告位,經測算廣告位出租收入是:線段![]() 處每千米為
處每千米為![]() 元,線段
元,線段![]() 及圓弧
及圓弧![]() 處每千米均為
處每千米均為![]() 元.設
元.設![]() 弧度,廣告位出租的總收入為
弧度,廣告位出租的總收入為![]() 元.
元.
(1)求![]() 關于
關于![]() 的函數解析式,并指出該函數的定義域;
的函數解析式,并指出該函數的定義域;
(2)試問:![]() 為何值時,廣告位出租的總收入最大?并求出其最大值.
為何值時,廣告位出租的總收入最大?并求出其最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面幾種推理是類比推理的( )
A. 兩條直線平行,同旁內角互補,如果![]() 和
和![]() 是兩條平行直線的同旁內角,則
是兩條平行直線的同旁內角,則![]()
B. 由平面三角形的性質,推測空間四邊形的性質
C. 某校高二級有20個班,1班有51位團員,2班有53位團員,3班有52位團員,由此可以推測各班都超過50位團員.
D. 一切偶數都能被2整除,![]() 是偶數,所以
是偶數,所以![]() 能被2整除.
能被2整除.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖、90后從事互聯網行業崗位分布條形圖,則下列結論中不一定正確的是( )
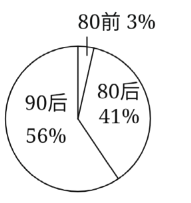
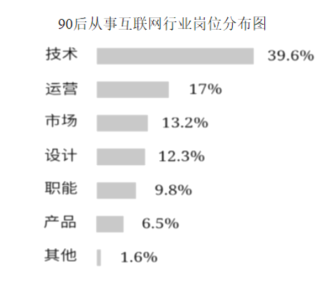
A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數超過總人數的20%
C.互聯網行業中從事運營崗位的人數90后比80后多
D.互聯網行業中從事運營崗位的人數90后比80前多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了實現1000萬元利潤的目標,準備制定一個激勵銷售人員的獎勵方案:在銷售利潤達到10萬元時,按銷售利潤進行獎勵,且獎勵金額y(單位:萬元)隨銷售利潤x(單位:萬元)的增加而增加,但獎金總數不超過5萬元,同時獎金不超過利潤的25%.現有三個獎勵模型:![]() ,
,![]() ,
,![]() ,其中哪個模型能符合公司的要求?
,其中哪個模型能符合公司的要求?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業常年生產一種出口產品,根據預測可知,進入![]() 世紀以來,該產品的產量平穩增長.記
世紀以來,該產品的產量平穩增長.記![]() 年為第
年為第![]() 年,且前
年,且前![]() 年中,第
年中,第![]() 年與年產量
年與年產量![]() 萬件之間的關系如下表所示:
萬件之間的關系如下表所示:
|
|
|
|
|
|
|
|
|
|
若![]() 近似符合以下三種函數模型之一:
近似符合以下三種函數模型之一:![]() ,
,![]() ,
,![]() .
.
(1)找出你認為最適合的函數模型,并說明理由,然后選取其中你認為最適合的數據求出相應的解析式;
(2)因遭受某國對該產品進行反傾銷的影響,![]() 年的年產量比預計減少
年的年產量比預計減少![]() ,試根據所建立的函數模型,確定
,試根據所建立的函數模型,確定![]() 年的年產量.
年的年產量.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com