
已知函數
 是定義在R上的奇函數,且當
是定義在R上的奇函數,且當 時不等式
時不等式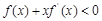 成立, 若
成立, 若 ,
,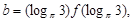
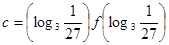 ,則
,則 的大小關系是 .
的大小關系是 .
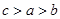
【解析】
試題分析:由已知式子(x)+xf′(x),可以聯想到:(uv)′=u′v+uv′,從而可設h(x)=xf(x),有:h′(x)=f(x)+xf′(x)<0,所以利用h(x)的單調性問題很容易解決。解:構造函數h(x)=xf(x),由函數y=f(x)以及函數y=x是R上的奇函數可得h(x)=xf(x)是R上的偶函數,又當x∈(-∞,0)時h′(x)=f(x)+xf′(x)<0,所以函數h(x)在x∈(-∞,0)時的單調性為單調遞減函數;所以h(x)在x∈(0,+∞)時的單調性為單調遞增函數.又因為函數y=f(x)是定義在R上的奇函數,所以f(0)=0,從而h(0)=0因為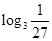 =-3,所以f(
=-3,所以f(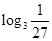 )=f(-3)=-f(3),由0<logπ3<1<50.5<30.5<2,所以h(logπ3)<h(50.5)<h(2)=f(
)=f(-3)=-f(3),由0<logπ3<1<50.5<30.5<2,所以h(logπ3)<h(50.5)<h(2)=f(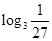 ),即:b<a<c,故答案為.
),即:b<a<c,故答案為.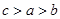
考點:函數奇偶性和單調性
點評:本題考查的考點與方法有:1)所有的基本函數的奇偶性;2)抽象問題具體化的思想方法,構造函數的思想;3)導數的運算法則:(uv)′=u′v+uv′;4)指對數函數的圖象;5)奇偶函數在對稱區間上的單調性:奇函數在對稱區間上的單調性相同;偶函數在對稱區間上的單調性相反;5)奇偶函數的性質:奇×奇=偶;偶×偶=偶;奇×偶=奇(同號得正、異號得負);奇+奇=奇;偶+偶=偶.本題結合已知構造出h(x)是正確解答的關鍵所在


科目:高中數學 來源:2012-2013學年浙江省紹興一中高二下學期期中考試理科數學試卷(帶解析) 題型:填空題
已知函數
 是定義在R上的奇函數,且當
是定義在R上的奇函數,且當 時不等式
時不等式 成立, 若
成立, 若 ,
,
 ,則
,則 的大小關系是 .
的大小關系是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com