
【題目】已知函數f(x)= ![]() (a,b∈R,且a≠0,e為自然對數的底數).
(a,b∈R,且a≠0,e為自然對數的底數).
(I)若曲線f(x)在點(e,f(e))處的切線斜率為0,且f(x)有極小值,求實數a的取值范圍.
(II)(i)當 a=b=l 時,證明:xf(x)+2<0;
(ii)當 a=1,b=﹣1 時,若不等式:xf(x)>e+m(x﹣1)在區間(1,+∞)內恒成立,求實數m的最大值.
【答案】解:(Ⅰ)∵f(x)= ![]() ,∴f′(x)=
,∴f′(x)= ![]() .
.
∵f′(e)=0,∴b=0,則f′(x)= ![]() .
.
當a>0時,f′(x)在(0,e)內大于0,在(e,+∞)內小于0,
∴f(x)在(0,e)內為增函數,在(e,+∞)內為減函數,即f(x)有極大值而無極小值;
當a<0時,f(x)在(0,e)內為減函數,在(e,+∞)內為增函數,即f(x)有極小值而無極大值.
∴a<0,即實數a的取值范圍為(﹣∞,0);
(Ⅱ)(i)證明:當a=b=1時,設g(x)=xf(x)+2=lnx﹣ex+2.
g′(x)= ![]() 在區間(0,+∞)上為減函數,又g′(1)=1﹣e<0,g′(
在區間(0,+∞)上為減函數,又g′(1)=1﹣e<0,g′( ![]() )=2﹣
)=2﹣ ![]() .
.
∴存在實數x0∈( ![]() ,1),使得
,1),使得 ![]() .
.
此時g(x)在區間(0,x0)內為增函數,在(x0 , +∞)內為減函數.
又 ![]() ,
,
∴ ![]() ,x0=﹣lnx0 .
,x0=﹣lnx0 .
由單調性知, ![]() =
= ![]() .
.
又x0∈( ![]() ,1),∴﹣(
,1),∴﹣( ![]() )<﹣2.
)<﹣2.
∴g(x)max<0,即xf(x)+2<0;
(ii)xf(x)>e+m(x﹣1)xf(x)﹣m(x﹣1)>e,
當 a=1,b=﹣1 時,設h(x)=xf(x)﹣m(x﹣1)=lnx+ex﹣m(x﹣1).
則h′(x)= ![]() .
.
令t(x)=h′(x)= ![]() .
.
∵x>1,∴t′(x)= ![]() .
.
∴h′(x)在(1,+∞)內單調遞增,
∴當x>1時,h′(x)>h′(1)=1+e﹣m.
①當1+e﹣m≥0時,即m≤1+e時,h′(x)>0,
∴h(x)在區間(1,+∞)內單調遞增,
∴當x>1時,h(x)>h(1)=e恒成立;
②當1+e﹣m<0時,即m>1+e時,h′(x)<0,
∴存在x0∈(1,+∞),使得h′(x0)=0.
∴h(x)在區間(1,x0)內單調遞減,在(x0 , +∞)內單調遞增.
由h(x0)<h(1)=e,
∴h(x)>e不恒成立.
綜上所述,實數m的取值范圍為(﹣∞,1+e].
∴實數m的最大值為:1+e.
【解析】(Ⅰ)求出原函數的導函數,由f′(e)=0得b=0,可得f′(x)= ![]() .然后對a分類討論,可知當a>0時,f(x)有極大值而無極小值;當a<0時,f(x)有極小值而無極大值.從而得到實數a的取值范圍為(﹣∞,0);(Ⅱ)(i)當a=b=1時,設g(x)=xf(x)+2=lnx﹣ex+2.求其導函數,可得g′(x)=
.然后對a分類討論,可知當a>0時,f(x)有極大值而無極小值;當a<0時,f(x)有極小值而無極大值.從而得到實數a的取值范圍為(﹣∞,0);(Ⅱ)(i)當a=b=1時,設g(x)=xf(x)+2=lnx﹣ex+2.求其導函數,可得g′(x)= ![]() 在區間(0,+∞)上為減函數,結合零點存在定理可得存在實數x0∈(
在區間(0,+∞)上為減函數,結合零點存在定理可得存在實數x0∈( ![]() ,1),使得
,1),使得 ![]() .得到g(x)在區間(0,x0)內為增函數,在(x0 , +∞)內為減函數.又
.得到g(x)在區間(0,x0)內為增函數,在(x0 , +∞)內為減函數.又 ![]() ,得
,得 ![]() ,x0=﹣lnx0 .
,x0=﹣lnx0 .
由單調性知g(x)max<0,即xf(x)+2<0;(ii)xf(x)>e+m(x﹣1)xf(x)﹣m(x﹣1)>e,當 a=1,b=﹣1 時,設h(x)=xf(x)﹣m(x﹣1)=lnx+ex﹣m(x﹣1).利用兩次求導可得當x>1時,h′(x)>h′(1)=1+e﹣m.然后分當1+e﹣m≥0時和當1+e﹣m<0時求解m的取值范圍.
【考點精析】通過靈活運用利用導數研究函數的單調性和函數的最大(小)值與導數,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值即可以解答此題.
比較,其中最大的是一個最大值,最小的是最小值即可以解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】為創建全國文明城市,某區向各事業行政單位征集“文明過馬路”義務督導員.從符合條件的600名志愿者中隨機抽取100名,按年齡作分組如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下頻率分布直方圖.
(Ⅰ)求圖中x的值,并根據頻率分布直方圖統計這600名志愿者中年齡在[30.40)的人數;
(Ⅱ)在抽取的100名志愿者中按年齡分層抽取10名參加區電視臺“文明伴你行”節目錄制,再從這10名志愿者中隨機選取3名到現場分享勸導制止行人闖紅燈的經歷,記這3名志愿者中年齡不低于35歲的人數為X,求X的分布列及數學期望.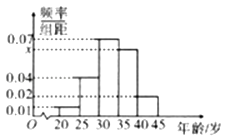
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓O:x2+y2=1過橢圓C: ![]() (a>b>0)的短軸端點,P,Q分別是圓O與橢圓C上任意兩點,且線段PQ長度的最大值為3. (Ⅰ)求橢圓C的方程;
(a>b>0)的短軸端點,P,Q分別是圓O與橢圓C上任意兩點,且線段PQ長度的最大值為3. (Ⅰ)求橢圓C的方程;
(Ⅱ)過點(0,t)作圓O的一條切線交橢圓C于M,N兩點,求△OMN的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)的表達式為f(x)= ![]() (c≠0),則函數f(x)的圖象的對稱中心為(﹣
(c≠0),則函數f(x)的圖象的對稱中心為(﹣ ![]() ,
, ![]() ),現已知函數f(x)=
),現已知函數f(x)= ![]() ,數列{an}的通項公式為an=f(
,數列{an}的通項公式為an=f( ![]() )(n∈N),則此數列前2017項的和為 .
)(n∈N),則此數列前2017項的和為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=2|x|﹣4的圖象與曲線C:x2+λy2=4恰有兩個不同的公共點,則實數λ的取值范圍是( )
A.[﹣ ![]() ,
, ![]() )
)
B.[﹣ ![]() ,
, ![]() ]
]
C.(﹣∞,﹣ ![]() ]∪(0,
]∪(0, ![]() )
)
D.(﹣∞,﹣ ![]() ]∪[
]∪[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知極坐標系的極點在直角坐標系的原點處,極軸與x軸非負半軸重合,直線l的參數方程為:  (t為參數),曲線C的極坐標方程為:ρ=4cosθ.
(t為參數),曲線C的極坐標方程為:ρ=4cosθ.
(1)寫出曲線C的直角坐標方程和直線l的普通方程;
(2)設直線l與曲線C相交于P,Q兩點,求|PQ|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數g(x)=|x|+2|x+2﹣a|(a∈R).
(1)當a=3時,解不等式g(x)≤4;
(2)令f(x)=g(x﹣2),若f(x)≥1在R上恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com