設關于x的方程(m+1)x2-mx+m-1=0有實根時實數m的取值范圍是集合A,函數的f(x)=lg[x2-(a+2)x+2a]定義域是集合B.
(1)求集合A; (2)若A∪B=B,求實數a的取值范圍.
【答案】
分析:(1)根據關于x的方程(m+1)x
2-mx+m-1=0有實根的充要條件,我們可求出實數m的取值范圍,得到集合A;
(2)根據對數函數中真數必須大于0的原則,我們可以求出集合B(含參數a),結合A∪B=B,即A⊆B求出實數a的取值范圍.
解答:解:(1)當m+l=0,即m=-1時,x-2=0.∴x=2,此時方程有實根.
當m+1≠0,即m≠-1時,由△=m
2-4(m+1)(m-1)≥0得3m
2-4≤0
解得
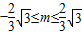
,此時

且m≠-l
綜上:A={m|
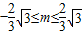
}
(2)∵A∪B=B,∴A⊆B
又B={x|x
2-(a+2)x+2a>0},
∴當a>2時,B={x|x<2或x>a},此時有A⊆B;
當a≤2時,B={x|x<a或x>2},
因為A⊆B,所以a>
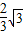
,此時2≥a>

綜上:a的取值范圍是(
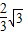
,+∞).
點評:本題考查的知識點是一元二次方程的根的分布與系數的關系,集合關系中的參數取值問題,對數函數的定義域,其中(1)中易忽略m=-1時,方程為一元一次方程滿足條件,(2)中要注意對a與2關系的分類討論.

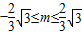 ,此時
,此時 且m≠-l
且m≠-l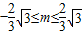 }
}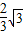 ,此時2≥a>
,此時2≥a>
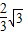 ,+∞).
,+∞).

 目標測試系列答案
目標測試系列答案