【題目】關于x的不等式ax﹣b＜0的解集是（1，+∞），則關于x的不等式（ax+b）（x﹣3）＞0的解集是（ ）
A.（﹣∞，﹣1）∪（3，+∞）
B.（1，3）
C.（﹣1，3）
D.（﹣∞，1）∪（3，+∞）
天天向上課時同步訓練系列答案
陽光課堂同步練習系列答案科目：高中數學 來源： 題型：
【題目】定義：若函數f（x）對于其定義域內的某一數x0 ， 有 f（x0）=x0 ， 則稱x0是f （x）的一個不動點．已知函數f（x）=ax2+（b+1）x+b﹣1 （a≠0）．
（1）當a=1，b=﹣2時，求函數f（x）的不動點；
（2）若對任意的實數b，函數f（x）恒有兩個不動點，求a的取值范圍；
（3）在（2）的條件下，若y=f（x）圖象上兩個點A，B的橫坐標是函數f（x）的不動點，且A，B兩點關于直線y=kx+ 
對稱，求b的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方形BCDE的邊長為a，已知AB= 
BC，將△ABE沿邊BE折起，折起后A點在平面BCDE上的射影為D點，則翻折后的幾何體中有如下描述： 
① AB與DE所成角的正切值是 
；
②AB∥CE
③VB﹣ACE體積是 
a3；
④平面ABC⊥平面ADC．
其中正確的有 ． （填寫你認為正確的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐P﹣ABC中，PC⊥平面ABC，∠ACB=45°，BC=2 
，AB=2．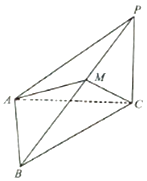 
（1）求AC的長；
（2）若PC= 
，點M在側棱PB上，且 
= 
，當λ為何值時，二面角B﹣AC﹣M的大小為30°．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，多面體ABCDPE的底面ABCD是平行四邊形，AD=AB=2， 
=0，PD⊥平面ABCD，EC∥PD，且PD=2EC=2，則二面角A﹣PB﹣E的大小為（ ）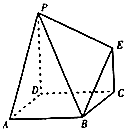 
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△ABC的三個內角A，B，C所對的邊分別為a，b，c，且asinAsinB+bcos2A= 
a．
（1）求 
；
（2）若c2=a2+ 
b2 ， 求角C．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）是奇函數，且對于任意x∈R滿足f（2﹣x）=f（x），當0＜x≤1時，f（x）=lnx+2，則函數y=f（x）在（﹣2，4]上的零點個數是（ ）
A.7
B.8
C.9
D.10
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，已知△ABC三個頂點坐標為A（7，8），B（10，4），C（2，﹣4）．
（1）求BC邊上的中線所在直線的方程；
（2）求BC邊上的高所在直線的方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
