
①(x2+y2)2=
(2)將下列曲線的極坐標方程化為直角坐標方程:
①ρ2=cos2θ;②ρ=![]() .
.
科目:高中數學 來源:2010年廣東省高一第二學期期末測試數學試題 題型:解答題
(本小題10分)“雪花曲線”因其形狀類似雪花而得名,它可以以下列方式產生,如圖,有一列曲線 ,已知
,已知 是邊長為1的等邊三角形,
是邊長為1的等邊三角形, 是對
是對 進行如下操作得到:將
進行如下操作得到:將 的每條邊三等分,以每邊中間部分的線段為邊,向外作等邊三角形,再將中間部分的線段去掉(
的每條邊三等分,以每邊中間部分的線段為邊,向外作等邊三角形,再將中間部分的線段去掉( ).
).

(1)記曲線 的邊長和邊數分別為
的邊長和邊數分別為 和
和 (
( ),求
),求 和
和 的表達式;
的表達式;
(2)記 為曲線
為曲線 所圍成圖形的面積,寫出
所圍成圖形的面積,寫出 與
與 的遞推關系式,并求
的遞推關系式,并求 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
①(x2+y2)2=
(2)將下列曲線的極坐標方程化為直角坐標方程:
①ρ2=cos2θ;②ρ=![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
①(x2+y2)2=2a2xy;②x-3y=0.
(2)將下列曲線的極坐標方程化為直角坐標方程:
①ρ2=cos2θ;②ρ=![]()
查看答案和解析>>
科目:高中數學 來源:2010年廣東省深圳高級中學高一第二學期期末測試數學試題 題型:解答題
(本小題10分)“雪花曲線”因其形狀類似雪花而得名,它可以以下列方式產生,如圖,有一列曲線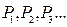 ,已知
,已知 是邊長為1的等邊三角形,
是邊長為1的等邊三角形, 是對
是對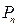 進行如下操作得到:將
進行如下操作得到:將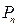 的每條邊三等分,以每邊中間部分的線段為邊,向外作等邊三角形,再將中間部分的線段去掉(
的每條邊三等分,以每邊中間部分的線段為邊,向外作等邊三角形,再將中間部分的線段去掉( ).
).
(1)記曲線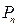 的邊長和邊數分別為
的邊長和邊數分別為 和
和 (
( ),求
),求 和
和 的表達式;
的表達式;
(2)記 為曲線
為曲線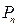 所圍成圖形的面積,寫出
所圍成圖形的面積,寫出 與
與 的遞推關系式,并求
的遞推關系式,并求 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com