
【題目】在![]() 中,D,E,F分別是邊
中,D,E,F分別是邊![]() ,
,![]() ,
,![]() 中點,下列說法正確的是( )
中點,下列說法正確的是( )
A.![]()
B.![]()
C.若 ,則
,則![]() 是
是![]() 在
在![]() 的投影向量
的投影向量
D.若點P是線段![]() 上的動點,且滿足
上的動點,且滿足![]() ,則
,則![]() 的最大值為
的最大值為![]()
【答案】BCD
【解析】
對選項A,B,利用平面向量的加減法即可判斷A錯誤,B正確.對選項C,首先根據已知得到![]() 為
為![]() 的平分線,即
的平分線,即![]() ,再利用平面向量的投影概念即可判斷C正確.對選項D,首先根據
,再利用平面向量的投影概念即可判斷C正確.對選項D,首先根據![]() 三點共線,設
三點共線,設![]() ,
,![]() ,再根據已知得到
,再根據已知得到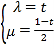 ,從而得到
,從而得到![]() ,即可判斷選項D正確.
,即可判斷選項D正確.
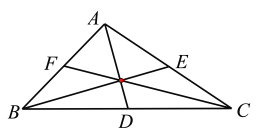
如圖所示:
對選項A,![]() ,故A錯誤.
,故A錯誤.
對選項B,![]()
![]()
![]() ,故B正確.
,故B正確.
對選項C,![]() ,
,![]() ,
,![]() 分別表示平行于
分別表示平行于![]() ,
,![]() ,
,![]() 的單位向量,
的單位向量,
由平面向量加法可知:![]() 為
為![]() 的平分線表示的向量.
的平分線表示的向量.
因為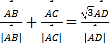 ,所以
,所以![]() 為
為![]() 的平分線,
的平分線,
又因為![]() 為
為![]() 的中線,所以
的中線,所以![]() ,如圖所示:
,如圖所示:

![]() 在
在![]() 的投影為
的投影為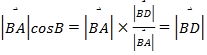 ,
,
所以![]() 是
是![]() 在
在![]() 的投影向量,故選項C正確.
的投影向量,故選項C正確.
對選項D,如圖所示:
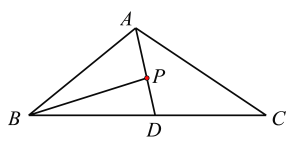
因為![]() 在
在![]() 上,即
上,即![]() 三點共線,
三點共線,
設![]() ,
,![]() .
.
又因為![]() ,所以
,所以![]() .
.
因為![]() ,則
,則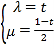 ,
,![]() .
.
令![]() ,
,
當![]() 時,
時,![]() 取得最大值為
取得最大值為![]() .故選項D正確.
.故選項D正確.
故選:BCD


科目:高中數學 來源: 題型:
【題目】如圖,在正三棱柱![]() 中,所有棱長都等于
中,所有棱長都等于![]() .
.

(1)當點![]() 是
是![]() 的中點時,
的中點時,
①求異面直線![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
②求二面角![]() 的正弦值;
的正弦值;
(2)當點![]() 在線段
在線段![]() 上(包括兩個端點)運動時,求直線
上(包括兩個端點)運動時,求直線![]() 與平面
與平面![]() 所成角的正弦值的取值范圍.
所成角的正弦值的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某自行車手從O點出發,沿折線O﹣A﹣B﹣O勻速騎行,其中點A位于點O南偏東45°且與點O相距20 ![]() 千米.該車手于上午8點整到達點A,8點20分騎至點C,其中點C位于點O南偏東(45°﹣α)(其中sinα=
千米.該車手于上午8點整到達點A,8點20分騎至點C,其中點C位于點O南偏東(45°﹣α)(其中sinα= ![]() ,0°<α<90°)且與點O相距5
,0°<α<90°)且與點O相距5 ![]() 千米(假設所有路面及觀測點都在同一水平面上).
千米(假設所有路面及觀測點都在同一水平面上).
(1)求該自行車手的騎行速度;
(2)若點O正西方向27.5千米處有個氣象觀測站E,假定以點E為中心的3.5千米范圍內有長時間的持續強降雨.試問:該自行車手會不會進入降雨區,并說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知四棱錐![]() 的底面
的底面![]() 為矩形,
為矩形, ![]() 底面
底面![]() ,且
,且![]() (
(![]() ),
),![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點.
的中點.

(1)當![]() 為何值時,平面
為何值時,平面![]() 平面
平面![]() ?并證明你的結論;
?并證明你的結論;
(2)當異面直線![]() 與
與![]() 所成角的正切值為2時,求三棱錐
所成角的正切值為2時,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在梯形ABCD中,DC∥AB,DC⊥CB,E是AB的中點,且AB=2BC=2CD=4(如圖所示),將△ADE沿DE翻折,使AB=2(如圖所示),F是線段AD上一點,且AF=2DF.
(Ⅰ)求四棱錐A-BCDE的體積;
(Ⅱ)在線段BE上是否存在一點G,使EF∥平面ACG?若存在,請指出點G的位置,并證明你的結論;若不存在,請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學在一次研究性學習中發現,以下五個式子的值都等于同一個常數:
①sin213°+cos217°﹣sin13°cos17°;
②sin215°+cos215°﹣sin15°cos15°;
③sin218°+cos212°﹣sin18°cos12°;
④sin2(﹣18°)+cos248°﹣sin(﹣18°)cos48°
⑤sin2(﹣25°)+cos255°﹣sin(﹣25°)cos55°
(Ⅰ)試從上述五個式子中選擇一個,求出這個常數;
(Ⅱ)根據(Ⅰ)的計算結果,將該同學的發現推廣為一三角恒等式sin2α+cos2(30°﹣α)﹣sinαcos(30°﹣α)= ,并證明你的結論.
(參考公式:sin(α±β)=sinαcosβ±cosαsinβ,cos(α±β)=cosαcosβsinαsinβsin2α=2sinαcosα,cos2α=cos2α﹣sin2α=2cos2α﹣1=1﹣2sin2α)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求方程![]() 的解集;
的解集;
(2)若關于x的方程![]() 在
在![]() 上恒有解,求m的取值范圍;
上恒有解,求m的取值范圍;
(3)若不等式![]() 在
在![]() 上恒成立,求m的取值范圍;
上恒成立,求m的取值范圍;
(4)若關于x的方程![]() 在
在![]() 上有解,那么當m取某一確定值時,方程所有解的和記為
上有解,那么當m取某一確定值時,方程所有解的和記為![]() ,求
,求![]() 所有可能值及相應的m的取值范圍.
所有可能值及相應的m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com