
已知4個命題:
①若等差數列 的前n項和為
的前n項和為 則三點
則三點 共線;
共線;
②命題:“ ”的否定是“
”的否定是“ ”;
”;
③若函數 在(0,1)沒有零點,則k的取值范圍是
在(0,1)沒有零點,則k的取值范圍是
④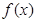 是定義在R上的奇函數,
是定義在R上的奇函數, 的解集為(
的解集為( 2,2)
2,2)
其中正確的是 。
①②④
解析試題分析:①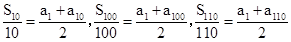 ,設等差數列的公差為d,
,設等差數列的公差為d,
∴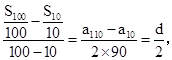
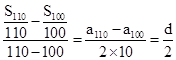 ,
,
即 前兩個點連線的斜率等于后兩個點連線的斜率,故三點共線,故①正確.
②根據命題的否定的定義,“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1≤3x”;是正確的,故②正確.
③函數 在(0,1)沒有零點,故f′(x)=1+
在(0,1)沒有零點,故f′(x)=1+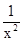 >0,所以函數在(0,1)內是增函數,x-
>0,所以函數在(0,1)內是增函數,x-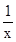 <0,當k≥2時,函數有零點,③不正確.
<0,當k≥2時,函數有零點,③不正確.
④f(x)是定義在R上的奇函數,f′(x)>0,且f(2)=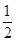 ,所以x>0時,函數是恒為正值,f(0)=0,x<0時函數為負值,2f(2)=1,則xf(x)<1的解集為(-2,2).正確.
,所以x>0時,函數是恒為正值,f(0)=0,x<0時函數為負值,2f(2)=1,則xf(x)<1的解集為(-2,2).正確.
故答案為:①②④.
考點:本題主要考查利用導數研究函數的單調性;命題的否定;函數零點的判定定理;三點共線.
點評:綜合題,考查三點共線,命題的否定,零點,導數與不等式的知識,考查知識的靈活應用能力,屬中檔題.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:高中數學 來源: 題型:填空題
已知兩點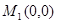 ,
,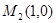 .以
.以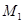 為圓心,
為圓心,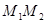 為半徑作圓交
為半徑作圓交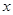 軸于點
軸于點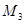 (異于
(異于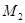 ),記作⊙
),記作⊙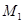 ;以
;以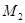 為圓心,
為圓心,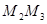 為半徑作圓交
為半徑作圓交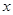 軸于點
軸于點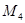 (異于
(異于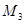 ),記作⊙
),記作⊙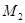 ;……;以
;……;以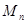 為圓心,
為圓心,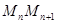 為半徑作圓交
為半徑作圓交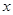 軸于點
軸于點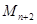 (異于
(異于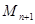 ),記作⊙
),記作⊙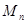 .當
.當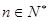 時,過原點作傾斜角為
時,過原點作傾斜角為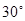 的直線與⊙
的直線與⊙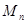 交于
交于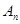 ,
,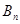 .考察下列論斷:
.考察下列論斷:
當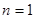 時,
時,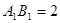 ;當
;當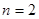 時,
時,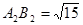 ;當
;當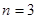 時,
時,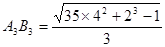 ;當
;當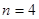 時,
時,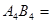 .
.
由以上論斷推測一個一般的結論:對于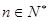 ,
,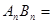 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
現有一根n節的竹竿,自上而下每節的長度依次構成等差數列,最上面一節長為 10cm,最下面的三節長度之和為114cm,第6節的長度是首節與末節長度的等比中項,則n= 。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某產品具有一定的時效性,在這個時效期內,由市場調查可知,在不做廣告宣傳且每件獲利a元的前提下,可賣出b件;若做廣告宣傳,廣告費為n千元比廣告費為 千元時多賣出
千元時多賣出 件。
件。
(1)試寫出銷售量 與n的函數關系式;
與n的函數關系式;
(2)當 時,廠家應該生產多少件產品,做幾千元的廣告,才能獲利最大?
時,廠家應該生產多少件產品,做幾千元的廣告,才能獲利最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com