Question

下圖中各圖表示的對應

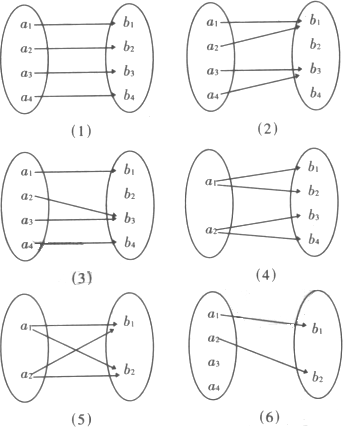
構成映射的個數是

[　　]

A．3

B．4

C．5

D．6

Answer 1

答案：A
解析：

解：(1)，(2)，(3)這三個圖所表示的對應都符合映射的定義，即A中每一個元素在對應法則下，B中都有唯一的元素與之對應． 　　對于(4)，(5)，A的每一個元素與B中有2個元素與之對應，所以不是A到B的映射．對于(6)，A中的元素a3，a4在B中沒有元素與之對應，所以不是A到B的映射． 　　綜上，可知能構成映射的個數為3． 　　思想方法小結：(1)從集合M到集合P的映射，是指按照某種對應法則f，對于集合M中的任何一個元素，在集合P中都有唯一的元素和它對應．由此可知，映射應滿足存在性(即集合M中的每一個元素在集合P中都有對應元素)和唯一性(即集合M中的每一個元素在集合P中都有唯一元素與之對應)． 　　(2)集合A到集合B中元素對應關系，可以是“多對一”、也可“一對一”，但不能“一對多”．

提示：

所謂映射，是指多對一的對應，一對一的對應，且A中的元素無剩余，以此判斷既準確，又迅速．