
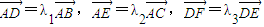 ,且
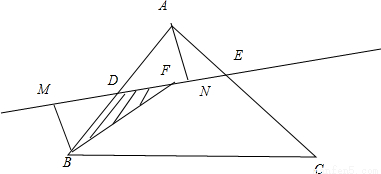
,且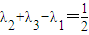 ,記△BDF的面積為s=f(λ1,λ2,λ3),則S的最大值是( )
,記△BDF的面積為s=f(λ1,λ2,λ3),則S的最大值是( )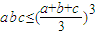 ,(當且僅當a=b=c時,取“=”)】
,(當且僅當a=b=c時,取“=”)】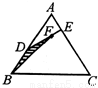




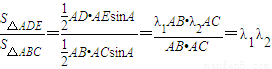 可求三角形ADE的面積,再由△DMB∽△DEA可得
可求三角形ADE的面積,再由△DMB∽△DEA可得 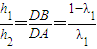 從而有
從而有 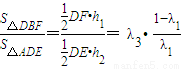 ,求出三角形DEF的面積之后,利用基本不等式可求面積的最大值
,求出三角形DEF的面積之后,利用基本不等式可求面積的最大值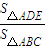 =
=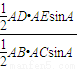 =λ1λ2
=λ1λ2 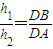 =
=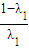
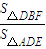 =
=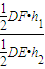 =
=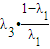
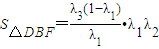 =λ2•λ3(1-λ1)
=λ2•λ3(1-λ1)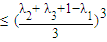 =
=
 取等號即S的最大值為
取等號即S的最大值為


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
| 2 |

查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=
如圖所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=| π | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
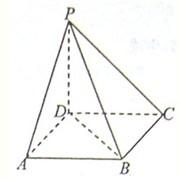 如圖所示,已知ABCD是正方形,邊長為2,PD⊥平面ABCD.
如圖所示,已知ABCD是正方形,邊長為2,PD⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:
如圖所示,已知正四棱錐S—ABCD側棱長為![]() ,底面邊長為
,底面邊長為![]() ,E是SA的中點,則異面直線BE與SC所成角的大小為 ( )
,E是SA的中點,則異面直線BE與SC所成角的大小為 ( )
A.90° B.60°
C.45° D.30°
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三一輪復習質量檢測理科數學 題型:選擇題
如圖所示,已知正四棱錐S—ABCD側棱長為 ,底面邊長為
,底面邊長為 ,E是SA的中點,則異面直線BE與SC所成角的大小為
( )
,E是SA的中點,則異面直線BE與SC所成角的大小為
( )
A.90° B.60° C.45° D.30°

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com