設f (x)是定義在[-1,1]上的偶函數,f (x)與g(x)的圖象關于x=1對稱,且當x∈[2,3]時,g(x)=a (x-2)-2 (x-2)3(a為常數).
(Ⅰ)求f (x)的解析式;
(Ⅱ)若f (x)在[0,1]上是增函數,求實數a的取值范圍;
(Ⅲ)若a∈(-6,6),問能否使f (x)的最大值為4?請說明理由.
【答案】
分析:(I)先根據f(x)與g(x)的圖象關于直線x=1對稱得出f(x)=g(2-x),根據g(x)的解析式,求出f(x)在[-1,0]上的解析式;再根據f(x)為偶函數得出f(x)在[-1,0]上的解析式.
(II)先求出f(x)在[0,1]上的導函數f’(x)=再根據其單調增可知f’(x)≥0,進而求出a的范圍.
(III)因為f(x)為偶函數,故只需考慮x∈[0,1],根據f(x)的導函數f’(x)=0,得出x的表達式,代入函數求得x=1,進而推斷函數的最大值不可能是4..
解答:解:(I)∵f(x)與g(x)的圖象關于直線x=1對稱,
∴f(x)=g(2-x).
∴當x∈[-1,0]時,2-x∈[2,3],
∴f(x)=g(2-x)=-ax+2x
3.
又∵f(x)為偶函數,
∴x∈[[0,1]時,-x∈[-1,0],
∴f(x)=f(-x)=ax-2x
3.
∴f(x)=

.
(II)∵f(x)為[0,1]上的增函數,
∴f’(x)=a-6x
2≥0Þa≥6x
2在區間[0,1]上恒成立.
∵x∈[0,1]時,6x
2≤6
∴a≥6,即a∈[6,+∞).
(III)由f(x)為偶函數,故只需考慮x∈[0,1],
由f′(x)=0得x=
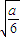
,
由f(

)=4Þa=6,
此時x=1,
當a∈(-6,6)時,f(x)的最大值不可能為4.
點評:本題主要考查函數的單調性和奇偶性的綜合運用.要利用好函數的對稱性和根據導函數的性質來判斷函數的單調性.

 .
.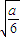 ,
, )=4Þa=6,
)=4Þa=6,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案