
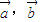 是兩個非零向量,且
是兩個非零向量,且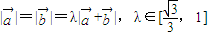 ,則
,則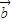 與
與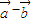 的夾角的取值范圍是 .
的夾角的取值范圍是 . 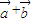 |=1,則|
|=1,則|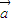 |=|
|=|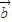 |=λ.令
|=λ.令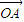 =
=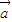 ,
,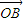 =
=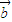 ,以OA、OB為臨邊作平行四邊形OACB,則平行四邊形OACB
,以OA、OB為臨邊作平行四邊形OACB,則平行四邊形OACB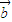 與
與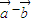 的夾角,即
的夾角,即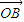 與
與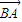 的夾角,等于π-θ,且0<θ<
的夾角,等于π-θ,且0<θ<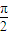 .△OAC中,由
.△OAC中,由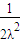 .再由
.再由 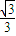 ≤λ≤1求得cos2θ的范圍,從而求得θ的范圍,即可得到
≤λ≤1求得cos2θ的范圍,從而求得θ的范圍,即可得到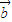 與
與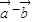 的
的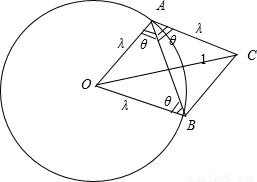 解:∵
解:∵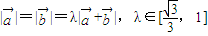 ,
,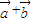 |=1,則|
|=1,則|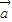 |=|
|=|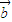 |=λ.
|=λ.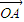 =
=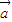 ,
, =
=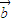 ,以OA、OB為鄰邊作平行四邊形OACB,
,以OA、OB為鄰邊作平行四邊形OACB, .
.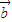 與
與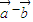 的夾角,即
的夾角,即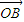 與
與 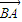 的夾角,
的夾角,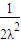 .
.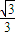 ≤λ≤1,可得
≤λ≤1,可得  ≤
≤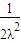 ≤
≤ ,∴-
,∴- ≤cos2θ≤
≤cos2θ≤ ,∴
,∴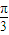 <2θ≤
<2θ≤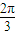 ,∴
,∴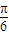 <θ≤
<θ≤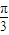 ,
,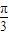 ≤π-θ<
≤π-θ<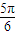 ,即
,即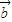 與
與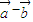 的夾角π-θ的取值范圍是[
的夾角π-θ的取值范圍是[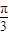 ,
,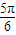 ).
).

 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com