
【題目】已知函數f(x)=mlnx﹣x2+2(m∈R).
(1)當m=1時,求f(x)的單調區間;
(2)若f(x)在x=1時取得極大值,求證:f(x)﹣f′(x)≤4x﹣3;
(3)若m≤8,當x≥1時,恒有f(x)﹣f′(x)≤4x﹣3恒成立,求m的取值范圍.
【答案】
(1)解:f(x)的定義域為(0,+∞), ![]() ,
,
解f′(x)=0,得 ![]() .當
.當 ![]() 時,f′(x)>0,f(x)單調遞增;
時,f′(x)>0,f(x)單調遞增;
當 ![]() 時,f′(x)<0,f(x)單調遞減.
時,f′(x)<0,f(x)單調遞減.
綜上,當m=1時,f(x)在 ![]() 上單調遞增,在
上單調遞增,在 ![]() 上單調遞減.
上單調遞減.
(2)解:若f(x)在x=1時取得極大值,則 ![]() ,則m=2.
,則m=2.
此時f(x)=2lnx﹣x2+2, ![]() .
.
令g(x)=f(x)﹣f′(x)﹣4x+3,
則 ![]() .
. ![]() .
.
令g′(x)=0,得x=±1.列表得
x | (0,1) | 1 | (1,+∞) |
g′(x) | + | 0 | ﹣ |
g(x) | ↗ | 極大值 | ↘ |
…(8分)
由上表知,gmax(x)=g(1)=0,所以g(x)≤0,即f(x)﹣f′(x)≤4x﹣3.
(3)解:令 ![]()
則 ![]() ①.
①.
當m≤2時,g′(x)<0,所以g(x)在(1,+∞)上單調遞減,所以當x≥1,g(x)≤
g(1),
故只需g(1)≤0,即﹣1﹣2﹣m+5≤0,即m≥2,所以m=2.
②當2<m≤8時,解g′(x)=0,得 ![]() .
.
當 ![]() 時,g′(x)>0,g(x)單調遞增;
時,g′(x)>0,g(x)單調遞增;
當 ![]() 時,g′(x)<0,g(x)單調遞減.
時,g′(x)<0,g(x)單調遞減.
所以當 ![]() 時,g(x)取得最大值.
時,g(x)取得最大值.
故只需 ![]() ,即
,即 ![]() ,
,
令 ![]() ,則
,則 ![]() ,
, ![]() ,
,
所以h′(x)在(1,+∞)上單調遞增,
又h′(1)=﹣2<0,h′(4)=ln4﹣1>0,以x0∈(1,4),h′(x0)=0,
所以h(x)在(1,x0)上單調遞減,
在(x0,4)上遞增,而h(1)=﹣1﹣4+5=0,h(4)=4ln4﹣4﹣8+5=8ln2﹣7<0,
所以x∈[1,4]上恒有h(x)≤0,
所以當2<m≤8時, ![]() .
.
綜上所述,2≤m≤8.
【解析】(1)f(x)的定義域為(0,+∞),求出函數的導數,利用f′(x)=0,求出極值點判斷函數的單調性,求出單調區間.(2)利用f(x)在x=1時取得極大值,求出m,令g(x)=f(x)﹣f′(x)﹣4x+3,通過函數的導數,求出函數的最值即可.(3)令 ![]() ,求出導函數,通過當m≤2時,g′(x)<0,當2<m≤8時,求出g(x)取得最大值.然后求解2≤m≤8.
,求出導函數,通過當m≤2時,g′(x)<0,當2<m≤8時,求出g(x)取得最大值.然后求解2≤m≤8.
【考點精析】關于本題考查的利用導數研究函數的單調性和函數的極值與導數,需要了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值才能得出正確答案.
是極小值才能得出正確答案.


 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)設![]() ,求證:數列
,求證:數列![]() 是等差數列,并求出
是等差數列,并求出![]() 的通項公式;
的通項公式;
(2)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,是否存在正整數
,是否存在正整數![]() ,使得
,使得![]() 對于
對于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,請說明理由.
的最小值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
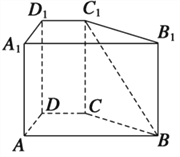
【題目】如圖,已知直四棱柱ABCD—A1B1C1D1中,AA1=2,底面ABCD是直角梯形,∠A為直角,AB∥CD,AB=4,AD=2,DC=2.
(Ⅰ)求線段BC1的長度;
(Ⅱ)異面直線BC1與DC所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+(lga+2)x+lgb滿足f(﹣1)=﹣2且對于任意x∈R,恒有f(x)≥2x成立.
(1)求實數a,b的值;
(2)解不等式f(x)<x+5.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD-A1B1C1D1中,M、N分別為棱BC和棱CC1的中點,則異面直線AC和MN所成的角為( )
A. 30° B. 45° C. 90° D. 60°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() cos(2x-
cos(2x-![]() ),x∈R.
),x∈R.
(1)求函數f(x)的最小正周期和單調遞減區間;
(2)求函數f(x)在區間[-![]() ,
,![]() ]上的最小值和最大值,并求出取得最值時x的值.
]上的最小值和最大值,并求出取得最值時x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查甲、乙兩種品牌商品的市場認可度,在某購物網點隨機選取了14天,統計在某確定時間段的銷量,得如下所示的統計圖,根據統計圖求:
(1)甲、乙兩種品牌商品銷量的中位數分別是多少?
(2)甲品牌商品銷量在[20,50]間的頻率是多少?
(3)甲、乙兩個品牌商品哪個更受歡迎?并說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的焦點是橢圓
的焦點是橢圓![]() 的頂點,
的頂點, ![]() 為橢圓
為橢圓![]() 的左焦點且橢圓
的左焦點且橢圓![]() 經過點
經過點 .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的右頂點
的右頂點![]() 作斜率為
作斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于另一點
于另一點![]() ,連結
,連結![]() 并延長
并延長![]() 交橢圓
交橢圓![]() 于點
于點![]() ,當
,當![]() 的面積取得最大值時,求
的面積取得最大值時,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com