Question

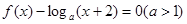設f(x)是定義在R的偶函數，對任意xÎR，都有f(x-2)=f(x+2)，且當xÎ[-2, 0]時， f(x)=．若在區間(-2,6]內關于x的方程恰有3個不同的實數根，則實數a的取值范圍是(    )

A．(1, 2)             B．(2,+¥)            C．(1,)           D．(, 2)

 

Answer 1

【答案】

B

【解析】

試題分析：畫出當x∈[-2，0]時，函數f（x）=的圖象（如圖）．

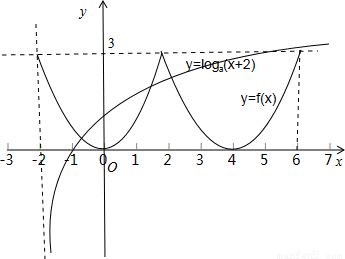
∵f（x）是定義在R上的偶函數，∴當x∈[0，2]時的函數f（x）的圖象與當x∈[-2，0]時，函數f（x）圖象關于y軸對稱．

∵對任意x∈R，都有f（x+2）=f（2-x）成立，∴函數f（x）的圖象關于直線x=2對稱．

根據以上的分析即可畫出函數y=f（x）在區間[-2，6]上的圖象．

當0＜a＜1時，可知不滿足題意，應舍去；

當a＞1時，畫出函數y=log_a（x+2）的圖象．

若使函數y=f（x）與y=log_a（x+2）=0在區間(-2,6]內有3個實根，而在（-2,0）必有一個實根，只需在區間（0，6]內恰有兩個不同的交點（即關于x的方程f（x）-log_a（x+2）=0在區間（0，6]內恰有兩個不同的實數根），則實數a滿足，log_a（6+2）＞3，

∴a³＜8，∴a＜2，又1＜a，∴1＜a＜2．故a的取值范圍為1＜a＜2．故選B．

考點：本題主要考查函數的奇偶性、周期性，指數函數、對數函數的性質。

點評：中檔題，此類題目在高考題中常常出現，綜合性較強，利用數形結合思想，提供分析圖形特征，形象直觀的使問題得解。