
【題目】已知函數![]() ,給出下列四個判斷:
,給出下列四個判斷:
(1)![]() 的值域是
的值域是![]() ;
;
(2)![]() 的圖像是軸對稱圖形;
的圖像是軸對稱圖形;
(3)![]() 的圖像是中心對稱圖形;
的圖像是中心對稱圖形;
(4)方程![]() 有解.
有解.
其中正確的判斷有( )
A.1個B.2個C.3個D.4個
科目:高中數學 來源: 題型:
【題目】為進一步優化教育質量平臺,更好的服務全體師生,七天網絡從甲、乙兩所學校各隨機抽取100名考生的某次“四省八校”數學考試成績進行分析,分別繪制的頻率分布直方圖如圖所示.
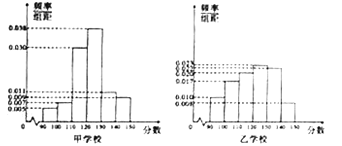
為了更好的測評各個學校數學學科的教學質量,該公司依據每一位考生的數學測試分數將其劃分為“![]() ,
,![]() ,
,![]() ”三個不同的等級,并按照不同的等級,設置相應的對學校數學學科教學質量貢獻的積分,如下表所示.
”三個不同的等級,并按照不同的等級,設置相應的對學校數學學科教學質量貢獻的積分,如下表所示.
測試分數 | 分數對應的等級 | 貢獻的積分 |
|
| 1分 |
|
| 2分 |
|
| 3分 |
(1)用樣本的頻率分布估計總體的頻率分布,若將甲學校考生的數學測試等級劃分為“![]() 等”和“非
等”和“非![]() 等”兩種,利用分層抽樣抽取10名考生,再從這10人隨機抽取3人,求3人中至少1人數學測試為“
等”兩種,利用分層抽樣抽取10名考生,再從這10人隨機抽取3人,求3人中至少1人數學測試為“![]() 等”的概率;
等”的概率;
(2)視頻率分布直方圖中的頻率為概率,用樣本估計總體,若從乙學校全體考生中隨機抽取3人,記3人中數學測試等級為“![]() 等”的人數為
等”的人數為![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() ;
;
(3)根據考生的數學測試分數對學校數學學科教學質量貢獻的積分規則,分別記甲乙兩所學校數學學科質量的人均積分為![]() 和
和![]() ,用樣本估計總體,求
,用樣本估計總體,求![]() 和
和![]() 的估計值,并以此分析,你認為哪所學校本次數學教學質量更加出色?
的估計值,并以此分析,你認為哪所學校本次數學教學質量更加出色?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點,焦點在x軸上的橢圓,離心率![]() ,且經過拋物線
,且經過拋物線![]() 的焦點.若過點
的焦點.若過點![]() 的直線
的直線![]() 斜率不等于零
斜率不等于零![]() 與橢圓交于不同的兩點E、
與橢圓交于不同的兩點E、![]() 在B、F之間
在B、F之間![]() ,
,
![]() 求橢圓的標準方程;
求橢圓的標準方程;
![]() 求直線l斜率的取值范圍;
求直線l斜率的取值范圍;
![]() 若
若![]() 與
與![]() 面積之比為
面積之比為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 的值域是
的值域是![]() ,有下列結論:①當
,有下列結論:①當![]() 時,
時,![]() ; ②當
; ②當![]() 時,
時,![]() ;③當
;③當![]() 時,
時,![]() ; ④當
; ④當![]() 時,
時,![]() .其中結論正確的所有的序號是( ).
.其中結論正確的所有的序號是( ).
A.①②B.③④C.②③D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合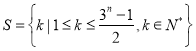 (
(![]() ,且
,且![]() ),若存在非空集合
),若存在非空集合![]() ,使得
,使得![]() ,且
,且![]() ,并任意
,并任意![]() ,都有
,都有![]() ,則稱集合S具有性質P,
,則稱集合S具有性質P,![]() 稱為集合S的P子集.
稱為集合S的P子集.
(1)當![]() 時,試說明集合S具有性質P,并寫出相應的P子集
時,試說明集合S具有性質P,并寫出相應的P子集![]() ;
;
(2)若集合S具有性質P,集合T是集合S的一個P子集,設![]() ,求證:任意
,求證:任意![]() ,
,![]() ,都有
,都有![]() ;
;
(3)求證:對任意正整數![]() ,集合S具有性質P.
,集合S具有性質P.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】英國統計學家E.H.辛普森1951年提出了著名的辛普森悖論,下面這個案例可以讓我們感受到這個悖論.有甲乙兩名法官,他們都在民事庭和行政庭主持審理案件,他們審理的部分案件被提出上訴.記錄這些被上述案件的終審結果如下表所示(單位:件):
法官甲 | 法官乙 | ||||||
終審結果 | 民事庭 | 行政庭 | 合計 | 終審結果 | 民事庭 | 行政庭 | 合計 |
維持 | 29 | 100 | 129 | 維持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合計 | 32 | 118 | 150 | 合計 | 100 | 25 | 125 |
記甲法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為![]() ,
,![]() 和
和![]() ,記乙法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為
,記乙法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為![]() ,
,![]() 和
和![]() ,則下面說法正確的是
,則下面說法正確的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,焦點為
上,焦點為![]() ,圓O的直徑為
,圓O的直徑為![]() .
.

(1)求橢圓C及圓O的標準方程;
(2)設直線l與圓O相切于第一象限內的點P,且直線l與橢圓C交于![]() 兩點.記
兩點.記![]() 的面積為
的面積為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 的前
的前![]() 項和為
項和為![]() 且滿足
且滿足![]() ,
,![]() (
(![]() 為常數,
為常數,![]() ).
).
(1)求![]() ;
;
(2)若數列![]() 是等比數列,求實數
是等比數列,求實數![]() 的值;
的值;
(3)是否存在實數![]() ,使得數列
,使得數列![]() 滿足:可以從中取出無限多項并按原來的先后次序排成一個等差數列?若存在,求出所有滿足條件的值;若不存在,請說明理由.
滿足:可以從中取出無限多項并按原來的先后次序排成一個等差數列?若存在,求出所有滿足條件的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com