
(12分)對于二次函數 ,
,
(1)指出圖像的開口方向、對稱軸方程、頂點坐標;
(2)求函數的最值;
(3)分析函數的單調性。
科目:高中數學 來源: 題型:解答題
已知二次函數 的最小值為1,且
的最小值為1,且 .
.
(1)求 的解析式;
的解析式;
(2)若 在區間
在區間 上不單調,求實數
上不單調,求實數 的取值范圍;
的取值范圍;
(3)在區間 上,
上,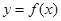 的圖像恒在
的圖像恒在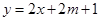 的圖像上方,試確定實數
的圖像上方,試確定實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
建造一條防洪堤,其斷面為等腰梯形,腰與底邊成角為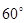 (如圖),考慮到防洪堤堅固性及石塊用料等因素,設計其斷面面積為
(如圖),考慮到防洪堤堅固性及石塊用料等因素,設計其斷面面積為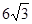 平方米,為了使堤的上面與兩側面的水泥用料最省,則斷面的外周長(梯形的上底線段
平方米,為了使堤的上面與兩側面的水泥用料最省,則斷面的外周長(梯形的上底線段 與兩腰長的和)要最小.
與兩腰長的和)要最小.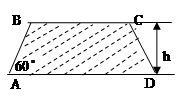
(1)求外周長的最小值,并求外周長最小時防洪堤高h為多少米?
(2)如防洪堤的高限制在 的范圍內,外周長最小為多少米?
的范圍內,外周長最小為多少米?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
商場銷售某一品牌的羊毛衫,購買人數是羊毛衫標價的一次函數,標價越高,購買人數越少.把購買人數為零時的最低標價稱為無效價格,已知無效價格為每件300元.現在這種羊毛衫的成本價是100元/ 件,商場以高于成本價的價格(標價)出售. 問:
(1)商場要獲取最大利潤,羊毛衫的標價應定為每件多少元?
(2)通常情況下,獲取最大利潤只是一種“理想結果”,如果商場要獲得最大利潤的75%,那么羊毛衫的標價為每件多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分10分)已知函數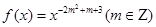 為偶函數,且在
為偶函數,且在 上為增函數.
上為增函數.
(1)求 的值,并確定
的值,并確定 的解析式;
的解析式;
(2)若 且
且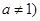 ,是否存在實數
,是否存在實數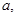 使
使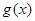 在區間
在區間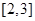 上的最大值為2,若存在,求出
上的最大值為2,若存在,求出 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)南昌市在加大城市化進程中,環境污染問題也日益突出。據環保局測定,某處的污染指數與附近污染源的強度成正比,與到污染源距離的平方成反比.現已知相距18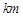 的A,B兩家工廠(視作污染源)的污染強度分別為
的A,B兩家工廠(視作污染源)的污染強度分別為 ,它們連線上任意一點C處的污染指數
,它們連線上任意一點C處的污染指數 等于兩家工廠對該處的污染指數之和.設
等于兩家工廠對該處的污染指數之和.設 (
(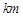 ).
).
(1) 試將 表示為
表示為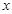 的函數;
的函數;
(2) 若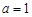 ,且
,且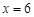 時,
時, 取得最小值,試求
取得最小值,試求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)="2" sin (0≤x≤5),點A、B分別是函數y=f(x)圖像上的最高點和最低點.
(0≤x≤5),點A、B分別是函數y=f(x)圖像上的最高點和最低點.
(1)求點A、B的坐標以及 ·
·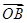 的值;
的值;
(2)沒點A、B分別在角 、
、 的終邊上,求tan(
的終邊上,求tan(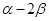 )的值.
)的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com