
【題目】在平面直角坐標系中,以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知直線
軸的正半軸為極軸建立極坐標系,已知直線![]() 上兩點
上兩點![]() 的極坐標分別為
的極坐標分別為 ,圓
,圓![]() 的參數(shù)方程為
的參數(shù)方程為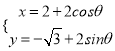 (
(![]() 為參數(shù)).
為參數(shù)).
(1)設(shè)![]() 為線段
為線段![]() 的中點,求直線
的中點,求直線![]() 的平面直角坐標方程;
的平面直角坐標方程;
(2)判斷直線![]() 與圓
與圓![]() 的位置關(guān)系.
的位置關(guān)系.
科目:高中數(shù)學 來源: 題型:
【題目】“拋階磚”是國外游樂場的典型游戲之一.參與者只需將手上的“金幣”(設(shè)“金幣”的半徑為1)拋向離身邊若干距離的階磚平面上,拋出的“金幣”若恰好落在任何一個階磚(邊長為2.1的正方形)的范圍內(nèi)(不與階磚相連的線重疊),便可獲大獎.不少人被高額獎金所吸引,紛紛參與此游戲,但很少有人得到獎品,請用所學的概率知識解釋這是為什么.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-5:不等式選講
已知函數(shù)![]()
(Ⅰ)求不等式![]() 的解集;
的解集;
(Ⅱ)已知函數(shù)![]() 的最小值為
的最小值為![]() ,若實數(shù)
,若實數(shù)![]() 且
且![]() ,求
,求![]() 的
的
最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某省電視臺為了解該省衛(wèi)視一檔成語類節(jié)目的收視情況,抽查東西兩部各5個城市,得到觀看該節(jié)目的人數(shù)(單位:千人)如下莖葉圖所示,其中一個數(shù)字被污損.
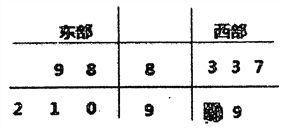
(I)求東部觀眾平均人數(shù)超過西部觀眾平均人數(shù)的概率.
(II)節(jié)目的播出極大激發(fā)了觀眾隨機統(tǒng)計了4位觀眾的周均學習成語知識的的時間y (單位:小時)與年齡x(單位:歲),并制作了對照表(如下表所示):

由表中數(shù)據(jù)分析,x,y呈線性相關(guān)關(guān)系,試求線性回歸方程![]() ,并預(yù)測年齡為60歲觀眾周均學習成語知識的時間.
,并預(yù)測年齡為60歲觀眾周均學習成語知識的時間.
參考數(shù)據(jù):線性回歸方程中![]() 的最小二乘估計分別是
的最小二乘估計分別是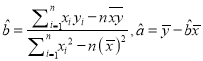 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某工廠對一批產(chǎn)品進行了抽樣檢測,如圖是根據(jù)抽樣檢測后的產(chǎn)品凈重(單位:克)數(shù)據(jù)繪制的頻率分布直方圖,其中產(chǎn)品凈重的范圍是[96,106],樣本數(shù)據(jù)分組為[96,98),[98,100),[100,102),[102,104),[104,106].已知樣本中產(chǎn)品凈重小于100克的個數(shù)是36,則樣本中凈重大于或等于98克并且小于104克的產(chǎn)品的個數(shù)是( )
A. 90 B. 75
C. 60 D. 45
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),將曲線
為參數(shù)),將曲線![]() 經(jīng)過伸縮變換
經(jīng)過伸縮變換![]() 后得到曲線
后得到曲線![]() .在以原點為極點,
.在以原點為極點, ![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)說明曲線![]() 是哪一種曲線,并將曲線
是哪一種曲線,并將曲線![]() 的方程化為極坐標方程;
的方程化為極坐標方程;
(2)已知點![]() 是曲線
是曲線![]() 上的任意一點,求點
上的任意一點,求點![]() 到直線
到直線![]() 的距離的最大值和最小值.
的距離的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)f(x)的最小值為-4,且關(guān)于x的不等式f(x)≤0的解集為{x|-1≤x≤3,x∈R}.
(1)求函數(shù)f(x)的解析式;
(2)求函數(shù)![]() 的零點個數(shù).
的零點個數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,側(cè)面
,側(cè)面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
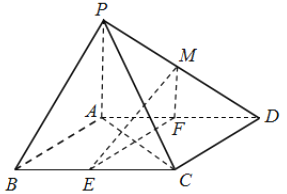
(1)求證: ![]() 平面
平面![]() ;
;
(2)如果直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)有一個正方形網(wǎng)格,其中每個最小正方形的邊長都為5 cm.現(xiàn)用直徑為2 cm的硬幣投擲到此網(wǎng)格上,求硬幣落下后與格線有公共點的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com