
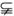
圖2-2-19
(1)求證:MNPQ是平行四邊形.
(2)若AC=BD,能截得菱形嗎,如何截?
(3)在什么情況下,可以截得一個矩形?
(4)在什么情況下,能截得一個正方形呢,如何截?
(5)若AC=BD=a,求證:平行四邊形MNPQ的周長一定.
思路分析:本題以線面、面面的平行為載體,來解決相關的問題.對于(1)可用兩組對邊分別平行來證明MNPQ是平行四邊形;再由比例的性質證得結論(2);當對棱垂直時,由空間等角的關系,可見四邊形MNPQ的一個角是直角,從而得到結(3);對于結論(4),只要滿足既是菱形又是矩形的要求即可;對于第(5)問,只要注意△AMQ∽△ABD,就可把平行四邊形MNPQ的周長表示出來,從而確定它是否是與a有關的定值.
(1)證明:∵AC∥平面MNPQ,且平面ADC∩平面MNPQ=PQ,且AC![]() 平面ADC,
平面ADC,
∴AC∥PQ.
同理可證AC∥MN,BD∥MQ,BD∥NP.
∴PQ∥MN,MQ∥NP.
∴四邊形MNPQ為一平行四邊形.
(2)解:由(1)得![]() ①
①
由MQ∥BD,得![]() .②
.②
又AC=BD,
①÷②得![]() ,當DQ=AQ時,
,當DQ=AQ時,
PQ=MQ.又四邊形MNPQ為平行四邊形,
∴MNPQ為菱形,即當Q取AD中點時可截得菱形.
(3)解:顯然,當AC⊥BD時,MN⊥NP,即四邊形MNPQ為矩形.
(4)解:由(2)和(3)可知,當AC=BD,且AC⊥BD,且Q為AD的中點時,四邊形MNPQ為一正方形.
(5)證明:設MQ=x,PQ=y,Q為AD上一點,且AQ∶QD=m∶n,
∵△AMQ∽△ABD,
∴![]() ,且BD=a.
,且BD=a.
∴x=MQ=![]() a.
a.
同理可得y=PQ=![]() a.
a.
∴x+y=![]() a+
a+![]() a=a.
a=a.
∴周長為2(x+y)=2a,
即當AC=BD=a時,平行四邊形MNPQ的周長為定值2a.
綠色通道:本小題是一道典型的發散性思維題,其中綜合了幾何中的多個知識點,特別是線面平行和線線平行.正確理解相關平面圖形的定義是解答本題的關鍵.通過引入了參數m、n、x、y,可建立相關量間的關系式,消去參數后即得所求結果.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com