
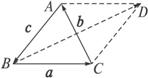
圖1
活動:教師引導學生回顧,向量具有二重性,一方面具有“形”的特點,因此有了幾何運算;另一方面又具有一套優良的代數運算性質,因此又有了代數運算.對于這兩種運算,前者難度大,靈活多變,對學生來說是個難點,后者學生感到熟悉,易于掌握,但應讓學生明了,這兩種方法都要掌握好,近幾年高考題的解答都是以兩種解法給出.本題給出的是三角形,對于某些幾何命題的抽象的證明,自然可以轉化為向量的幾何運算問題來解決,請同學們在探究中要注意仔細體會,領悟其實質.教學中,教師要放手大膽地讓學生自己去探究,鼓勵學生從不同的角度去觀察、去發現.真正做到一題多用,一題多變,串聯知識,串聯方法,使學生在探究過程中掌握孤零知識,提高思維能力,提高復習效率.
證法一:由題意,得a+b+c=0,∴c=-(a+b).
又∵b·c=c·a,∴c·(a-b)=0.
∴-a2+b2=0.∴|a|2=|b|2,即|a|=|b|.
同理可得|c|=|b|,∴|a|=|b|=|c|.
∴△ABC為正三角形.
證法二:由題意得a+b+c=0,∴a=-b-c,b=-a-c.
∴a2=b2+c2+2b·c,b2=a2+c2+2a·c.
而b·c=c·a(已知),
∴a2-b2=b2-a2.
∴a2=b2.∴|a|2=|b|2.
∴|a|=|b|.
同理可得|c|=|b|,∴|a|=|b|=|c|.
∴△ABC為正三角形.

圖2
證法三:如圖2,以AB,BC為鄰邊作![]() ABCD,則
ABCD,則![]() =a,
=a,![]() =
=![]() -
-![]() ,
,
∴![]() =a-c.
=a-c.
又∵a·b=b·c,∴b·(a-c)=0.
∴b·![]() =0.∴b⊥
=0.∴b⊥![]() .
.
∴![]() ABCD為菱形.∴AB=BC.同理可得BC=AC,
ABCD為菱形.∴AB=BC.同理可得BC=AC,
∴△ABC為正三角形.
證法四:取![]() 的中點E,連接AE,則
的中點E,連接AE,則
![]() =
=![]() (
(![]() +
+![]() )=
)=![]() (c-b),
(c-b),
∴![]() ·a=
·a=![]() (c-b)·a=0.
(c-b)·a=0.
∴![]() ⊥a.∴AB=AC.
⊥a.∴AB=AC.
同理可得BC=AC,
∴△ABC為正三角形.
點評:本題給出了四種證法,教師要善于引導學生進行一題多解,這是一種很有效的辦法.數學教學中,一題多解訓練是培養學生思維靈活的一種良好手段.通過一題多解的訓練能溝通知識之間的內在聯系,提高學生應用所學的基礎知識與基本技能解決實際問題的能力,逐步學會舉一反三的本領,在教材安排的例題中,有相當一部分題目存在一題多解的情況,教師要引導學生善于挖掘.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
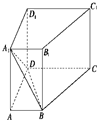 如圖,已知在直四棱柱ABCD-A1B1C1D1中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如圖,已知在直四棱柱ABCD-A1B1C1D1中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.查看答案和解析>>
科目:高中數學 來源: 題型:
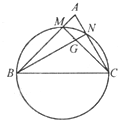 (2013•成都一模)如圖,已知在△ABC中,BC=2,以BC為直徑的圓分別交AB,AC于點M,N,MC與NB交于點G,若
(2013•成都一模)如圖,已知在△ABC中,BC=2,以BC為直徑的圓分別交AB,AC于點M,N,MC與NB交于點G,若| BM |
| BC |
| CN |
| BC |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•杭州二模)如圖,已知在四棱錐P-ABCD中,底面ABCD是平行四邊形,PA⊥平面ABCD,PA=
(2013•杭州二模)如圖,已知在四棱錐P-ABCD中,底面ABCD是平行四邊形,PA⊥平面ABCD,PA=| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
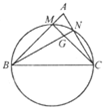 如圖,已知在△ABC中,BC=2,以BC為直徑的圓分別交AB,AC于點M,N,MC與NB交于點G,若
如圖,已知在△ABC中,BC=2,以BC為直徑的圓分別交AB,AC于點M,N,MC與NB交于點G,若| BM |
| BC |
| CN |
| BC |
查看答案和解析>>
科目:高中數學 來源: 題型:
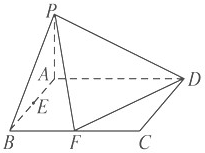 如圖,已知在四棱錐PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分別是線段AB,BC的中點.
如圖,已知在四棱錐PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分別是線段AB,BC的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com