
 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
| 1 |
| 2x |
| 1 |
| 2 |
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | x2 |
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省青島市高三統一質量檢測考試理科數學試卷(解析版) 題型:選擇題
在實數集 中定義一種運算“
中定義一種運算“ ”,對任意
”,對任意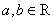 ,
,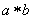 為唯一確定的實數,且具有性質:
為唯一確定的實數,且具有性質:
(1)對任意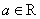 ,
, ;
;
(2)對任意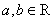 ,
,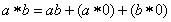 .
.
關于函數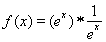 的性質,有如下說法:①函數
的性質,有如下說法:①函數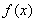 的最小值為
的最小值為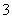 ;②函數
;②函數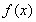 為偶函數;③函數
為偶函數;③函數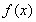 的單調遞增區間為
的單調遞增區間為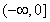 .
.
其中所有正確說法的個數為( )
A.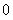 B.
B.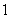 C.
C.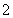 D.
D.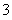
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com