
【題目】(1)兩個共軛復數的差是純虛數;(2)兩個共軛復數的和不一定是實數;(3)若復數a+bi(a,b∈R)是某一元二次方程的根,則a﹣bi是也一定是這個方程的根;(4)若z為虛數,則z的平方根為虛數,
其中正確的個數為( )
A.3
B.2
C.1
D.0
【答案】C
【解析】解:(1)兩個共軛復數的差是純虛數;如果兩個復數是實數,差值也是實數,所以(1)不正確;(2)兩個共軛復數的和不一定是實數;不正確,和一定是實數;(3)若復數a+bi(a,b∈R)是某一元二次方程的根,則a﹣bi是也一定是這個方程的根;不正確,因為實系數方程的虛根是共軛復數,所以(3)不正確;(4)若z為虛數,則z的平方根為虛數,如果虛數為i,則設z=x+yi(x,y∈R),
由z2=(x+yi)2=i,得x2﹣y2+2xyi=i,
∴ ![]() ,解得:
,解得: 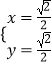 或
或 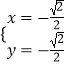 .
.
∴z= ![]() +
+ ![]() i或z=﹣
i或z=﹣ ![]() ﹣
﹣ ![]() i.
i.
所以正確.
故選:C.
【考點精析】本題主要考查了命題的真假判斷與應用和復數的定義的相關知識點,需要掌握兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系;形如![]() 的數叫做復數,
的數叫做復數,![]() 和
和![]() 分別叫它的實部和虛部才能正確解答此題.
分別叫它的實部和虛部才能正確解答此題.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
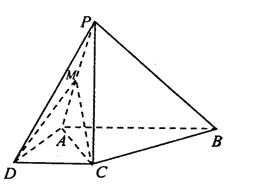
(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() 為線段
為線段![]() 的中點,且過
的中點,且過![]() 三點的平面與線段
三點的平面與線段![]() 交于點
交于點![]() ,確定點
,確定點![]() 的位置,說明理由;并求三棱錐
的位置,說明理由;并求三棱錐![]() 的高.
的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log2x,x∈(4,8),則函數y=f(x2)+ ![]() 的值域為( )
的值域為( )
A.[8,10)
B.( ![]() ,10)
,10)
C.(8, ![]() )
)
D.( ![]() ,10)
,10)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題P:方程x2+mx+1=0有兩個不等的實數根,命題q:方程4x2+4(m﹣2)x+1=0無實數根.若p∧q為假,若p∨q為真,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
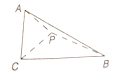
【題目】已知直角三角形![]() 的兩條直角邊
的兩條直角邊![]() ,
, ![]() ,
, ![]() 為斜邊
為斜邊![]() 上一點,沿
上一點,沿![]() 將三角形折成直二面角
將三角形折成直二面角![]() ,此時二面角
,此時二面角![]() 的正切值為
的正切值為![]() ,則翻折后
,則翻折后![]() 的長為( )
的長為( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】動圓M與圓(x﹣1)2+y2=1相外切且與y軸相切,則動圓M的圓心的軌跡記C,
(1)求軌跡C的方程;
(2)定點A(3,0)到軌跡C上任意一點的距離|MA|的最小值;
(3)經過定點B(﹣2,1)的直線m,試分析直線m與軌跡C的公共點個數,并指明相應的直線m的斜率k是否存在,若存在求k的取值或取值范圍情況[要有解題過程,沒解題方程只有結論的只得結論分].
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+ ![]() ﹣4,g(x)=kx+3.
﹣4,g(x)=kx+3.
(1)當a=k=1時,求函數y=f(x)+g(x)的單調遞增與單調遞減區間;
(2)當a∈[3,4]時,函數f(x)在區間[1,m]上的最大值為f(m),試求實數m的取值范圍;
(3)當a∈[1,2]時,若不等式|f(x1)|﹣|f(x2)|<g(x1)﹣g(x2)對任意x1 , x2∈[2,4](x1<x2)恒成立,求實數k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com