Question

已知集合M={（a+3）+（b²-1）i，8}，集合N={3i，（a²-1）+（b+2）i}，其中a，b∈R，i是虛數單位，若M=N，則

1. A.
   a=-3，b=-2
2. B.
   a=-3，b=2
3. C.
   a=±3，b=-2
4. D.
   a=3，b=2

Answer 1

A
分析：由題意，兩個集合滿足M=N，即兩個集合中的元素是相同的，由M={（a+3）+（b²-1）i，8}，集合N={3i，（a²-1）+（b+2）i}，其中a，b∈R，i是虛數單位，易得出a，b滿足的方程，從中解出它們的值即可先出正確選項
解答：由題意M={（a+3）+（b²-1）i，8}，集合N={3i，（a²-1）+（b+2）i}，其中a，b∈R，i是虛數單位，M=N
∴，
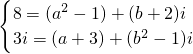
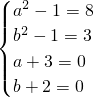
∴，解得a=-3，b=-2
故選A
點評：本題考查集合的相等，復數的相等條件，解題的關鍵是理解集合相等的意義，復數相等的條件，由這些知識轉化出參數a，b所滿足的方程是本題的難點，本題是集合的基本運算題