
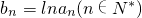 ,數列{bn}的前n項和為Sn,對于給定的正整數m,如果
,數列{bn}的前n項和為Sn,對于給定的正整數m,如果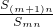 的值與n無關,求k的值.
的值與n無關,求k的值.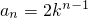 .
. =n[ln2+
=n[ln2+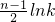 ].
].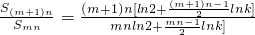
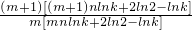 ,
,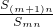 的值是一個與n無關的量,
的值是一個與n無關的量, =
=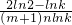 ,
,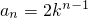 .所以{bn}是首項為ln2,公差為lnk的等差數列.由此入手能夠求出實數k.
.所以{bn}是首項為ln2,公差為lnk的等差數列.由此入手能夠求出實數k.

 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 1-x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com