
【題目】已知函數![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)已知![]() 為
為![]() 的兩個零點,證明:
的兩個零點,證明:![]() .
.
【答案】(1)見解析(2)見解析
【解析】分析:(1)首先確定函數的定義域,之后對函數求導,對參數![]() 進行討論,當導數大于零時單調增,當導數小于零時單調減;
進行討論,當導數大于零時單調增,當導數小于零時單調減;
(2)由函數有兩個零點,根據第一問的結論,可以斷定![]() ,分別將兩個零點代入函數解析式,得到兩個方程,將兩式相減得到
,分別將兩個零點代入函數解析式,得到兩個方程,將兩式相減得到![]() ,即
,即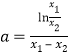 ,之后將問題轉化,構造新函數,利用導數研究函數的性質,從而證得結果.
,之后將問題轉化,構造新函數,利用導數研究函數的性質,從而證得結果.
詳解:(1)函數![]() 的定義域為
的定義域為![]() ,
,
![]() ,
,
當![]() 時
時![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,
令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
∴![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 上單調遞減.
上單調遞減.
(2)由![]() 為
為![]() 的兩個零點及(1)知
的兩個零點及(1)知![]() ,
,
∴![]() ,兩式相減得
,兩式相減得![]() ,即
,即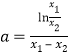 ,
,
要證![]() ,只需證
,只需證![]() ,
,
即證 ,即證
,即證![]()
![]() ,
,
不妨設![]() ,令
,令![]() ,只需證
,只需證![]() ,
,
設![]() ,則
,則![]()
![]() ,
,
設![]() ,則
,則![]() ,∴
,∴![]() 在
在![]() 上單減,
上單減,
∴![]() ,∴
,∴![]() 在
在![]() 上單增,
上單增,
∴![]() ,即
,即![]() 在
在![]() 時恒成立,原不等式得證.
時恒成立,原不等式得證.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】已知四面體P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC= ![]() AB,若四面體P﹣ABC的體積為
AB,若四面體P﹣ABC的體積為 ![]() ,則該球的體積為( )
,則該球的體積為( )
A.![]()
B.2π
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“開門大吉”是某電視臺推出的游戲節目.選手面對1~8號8扇大門,依次按響門上的門鈴,門鈴會播放一段音樂(將一首經典流行歌曲以單音色旋律的方式演繹),選手需正確回答出這首歌的名字,方可獲得該扇門對應的家庭夢想基金.在一次場外調查中,發現參賽選手多數分為兩個年齡段:20~30;30~40(單位:歲),其猜對歌曲名稱與否的人數如圖所示. 
(1)寫出2×2列聯表;判斷是否有90%的把握認為猜對歌曲名稱與否和年齡有關;說明你的理由;(下面的臨界值表供參考) (參考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)現計劃在這次場外調查中按年齡段選取6名選手,并抽取3名幸運選手,求3名幸運選手中在20~30歲之間的人數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在亞丁灣海域執行護航任務的中國海軍“徐州”艦,在A處收到某商船在航行中發出求救信號后,立即測出該商船在方位角方位角(是從某點的指北方向線起,依順時針方向到目標方向線之間的水平夾角)為45°、距離A處為10 n mile的C處,并測得該船正沿方位角為105°的方向,以9 n mile/h的速度航行,“徐州”艦立即以21 n mile/h的速度航行前去營救.
(1)“徐州”艦最少需要多少時間才能靠近商船?
(2)在營救時間最少的前提下,“徐州”艦應按照怎樣的航行方向前進?(角度精確到0.1°,時間精確到1min,參考數據:sin68.2°≈0.9286)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)在(﹣1,+∞)上單調,且函數y=f(x﹣2)的圖象關于x=1對稱,若數列{an}是公差不為0的等差數列,且f(a50)=f(a51),則{an}的前100項的和為( )
A.﹣200
B.﹣100
C.0
D.﹣50
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別是角A,B,C的對邊,b= ![]() sinB,且滿足tanA+tanC=
sinB,且滿足tanA+tanC= ![]() . (Ⅰ)求角C和邊c的大小;
. (Ⅰ)求角C和邊c的大小;
(Ⅱ)求△ABC面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx+x(x﹣a)2(a∈R),若存在 ![]() ,使得f(x)>xf'(x)成立,則實數a的取值范圍是( )
,使得f(x)>xf'(x)成立,則實數a的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.(3,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=a lnx+![]() +x (a≠0).
+x (a≠0).
(1)若曲線y=f (x)在點(1,f (1))處的切線與直線x-2y=0垂直,求實數a的值;
(2)討論函數f (x)的單調性.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com