
【題目】下列說法正確的是( )
A.“![]() ”是“點
”是“點![]() 到直線
到直線![]() 的距離為3”的充要條件
的距離為3”的充要條件
B.直線![]() 的傾斜角的取值范圍為
的傾斜角的取值范圍為![]()
C.直線![]() 與直線
與直線![]() 平行,且與圓
平行,且與圓![]() 相切
相切
D.離心率為![]() 的雙曲線的漸近線方程為
的雙曲線的漸近線方程為![]()
【答案】BC
【解析】
根據點到直線的距離公式判斷選項A錯誤;根據直線斜率的定義及正切函數的值域問題判斷選項B正確;根據兩直線平行的判定及直線與圓相切的判定,可判斷選項C正確;根據雙曲線漸近線的定義可判斷選項D錯誤.
選項A:由點![]() 到直線
到直線![]() 的距離為3,
的距離為3,
可得:![]() ,解得
,解得![]() 或
或![]() ,
,
“![]() ”是“點
”是“點![]() 到直線
到直線![]() 的距離為3”的充分不必要條件,
的距離為3”的充分不必要條件,
故選項A錯誤;
選項B:直線![]() 的斜率
的斜率![]() ,
,
設直線的傾斜角為![]() ,則
,則![]() 或
或![]() ,
,
![]() ,故選項B正確;
,故選項B正確;
選項C:直線![]() 可化為
可化為![]() ,
,
其與直線![]() 平行,
平行,
圓![]() 的圓心
的圓心![]() 到直線
到直線![]() 的距離為:
的距離為:
![]() ,
,
則直線![]() 與圓
與圓![]() 相切,故選項C正確;
相切,故選項C正確;
選項D:離心率為![]() ,則
,則![]()
若焦點在x軸,則雙曲線的漸近線方程為![]() ,
,
若焦點在y軸,則雙曲線的漸近線方程為![]() ,
,
故選項D錯誤.
故選:BC.


科目:高中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,沿中位線DE折起后,點A對應的位置為點P,
,沿中位線DE折起后,點A對應的位置為點P,![]() .
.
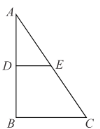
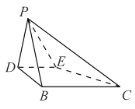
(1)求證:平面![]() 平面DBCE;
平面DBCE;
(2)求證:平面![]() 平面PCE;
平面PCE;
(3)求直線BP與平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自2017年7月27日上映以來,《戰狼2》的票房一路高歌猛進,并不斷刷新華語電影票房紀錄.繼8月25日官方宣布沖破53億票房之后,根據外媒Worldwide Box Office給出的2017年周末全球票房最新排名,《戰狼2》以8.151億美元(約54.18億元)的成績成功殺入前五.通過收集并整理了《戰狼2》上映前兩周的票房(單位:億元)數據,繪制出下面的條形圖.根據該條形圖,下列結論錯誤的是( )
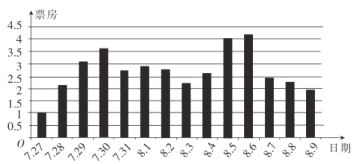
A.在《戰狼2》上映前兩周中,前四天票房逐日遞增
B.在《戰狼2》上映前兩周中,日票房超過2億元的共有12天
C.在《戰狼2》上映前兩周中,8月5日,8月6日達到了票房的高峰期
D.在《戰狼2》上映前兩周中,前五日的票房平均數高于后五日的票房平均數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a是實數,關于z的方程(z2-2z+5)(z2+2az+1)=0有4個互不相等的根,它們在復平面上對應的4個點共圓,則實數a的取值范圍是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圖![]() :
:![]() 的右頂點與拋物線
的右頂點與拋物線![]() :
:![]() 的焦點重合,橢圓
的焦點重合,橢圓![]() 的離心率為
的離心率為![]() ,過橢圓
,過橢圓![]() 的右焦點
的右焦點![]() 且垂直于
且垂直于![]() 軸的直線截拋物線所得的弦長為
軸的直線截拋物線所得的弦長為![]() .
.
(1)求橢圓![]() 和拋物線
和拋物線![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() .當直線
.當直線![]() 繞點
繞點![]() 旋轉時,直線
旋轉時,直線![]() 是否經過一定點?請判斷并證明你的結論.
是否經過一定點?請判斷并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點;當直線
兩點;當直線![]() 經過橢圓
經過橢圓![]() 的下頂點
的下頂點![]() 和右焦點
和右焦點![]() 時,
時,![]() 的周長為
的周長為![]() ,且
,且![]() 與橢圓
與橢圓![]() 的另一個交點的橫坐標為
的另一個交點的橫坐標為![]()
(1)求橢圓![]() 的方程;
的方程;
(2)點![]() 為
為![]() 內一點,
內一點,![]() 為坐標原點,滿足
為坐標原點,滿足![]() ,若點
,若點![]() 恰好在圓
恰好在圓![]() 上,求實數
上,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中任選一個,補充在下面問題中,若問題中的正整數k存在,求k的值;若k不存在,請說明理由.
這三個條件中任選一個,補充在下面問題中,若問題中的正整數k存在,求k的值;若k不存在,請說明理由.
設![]() 為等差數列
為等差數列![]() 的前n項和,
的前n項和,![]() 是等比數列,______,
是等比數列,______,![]() ,
,![]() ,
,![]() .是否存在k,使得
.是否存在k,使得![]() 且
且![]() ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“割圓術”是我國古代計算圓周率![]() 的一種方法.在公元
的一種方法.在公元![]() 年左右,由魏晉時期的數學家劉徽發明.其原理就是利用圓內接正多邊形的面積逐步逼近圓的面積,進而求
年左右,由魏晉時期的數學家劉徽發明.其原理就是利用圓內接正多邊形的面積逐步逼近圓的面積,進而求![]() .當時劉微就是利用這種方法,把
.當時劉微就是利用這種方法,把![]() 的近似值計算到
的近似值計算到![]() 和
和![]() 之間,這是當時世界上對圓周率
之間,這是當時世界上對圓周率![]() 的計算最精確的數據.這種方法的可貴之處就是利用已知的、可求的來逼近未知的、要求的,用有限的來逼近無窮的.為此,劉微把它概括為“割之彌細,所失彌少,割之又割,以至于不可割,則與圓合體,而無所失矣”.這種方法極其重要,對后世產生了巨大影響,在歐洲,這種方法后來就演變為現在的微積分.根據“割圓術”,若用正二十四邊形來估算圓周率
的計算最精確的數據.這種方法的可貴之處就是利用已知的、可求的來逼近未知的、要求的,用有限的來逼近無窮的.為此,劉微把它概括為“割之彌細,所失彌少,割之又割,以至于不可割,則與圓合體,而無所失矣”.這種方法極其重要,對后世產生了巨大影響,在歐洲,這種方法后來就演變為現在的微積分.根據“割圓術”,若用正二十四邊形來估算圓周率![]() ,則
,則![]() 的近似值是( )(精確到
的近似值是( )(精確到![]() )(參考數據
)(參考數據![]() )
)

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com