Question

【題目】某中學為研究學生的身體素質與體育鍛煉時間的關系，對該校200名高二學生平均每天體育鍛煉的時間進行調查，調查結果如下表，將學生日均體育鍛煉時間在的學生評價為“鍛煉達標”.

平均每天鍛煉的時間/分鐘
總人數	20	36	44	50	40	10

（1）請根據上述表格中的統計數據填寫下面2×2列聯表；并通過計算判斷，是否能在犯錯誤的概率不超過0.025的前提下認為“鍛煉達標”與性別有關？

	鍛煉不達標	鍛煉達標	合計
男
女		20	110
合計

（2）在“鍛煉達標”的學生中，按男女用分層抽樣方法抽出5人，進行體育鍛煉體會交流，

（ⅰ）求這5人中，男生、女生各有多少人？

（ⅱ）從參加體會交流的5人中，隨機選出3人作重點發言，求選出的這3人中至少有1名女生的概率.

參考公式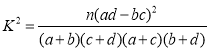：，其中.

臨界值表：

	0.10	0.05	0.025	0.010
	2.706	3.841	5.024	6.635

Answer 1

【答案】（1）表格見解析，能；（2）（ⅰ）男生3人，女生2人；（ⅱ）

【解析】

（1）由鍛煉達標人數為50及總人數為200，可完成表格，代入公式，算得結果與5.024作比較，即可得到本題答案；（2）先按比例算出5人中男女的人數，然后用列舉法解決古典概型問題.

解：（1）列出列聯表，如下：

	鍛煉不達標	鍛煉達標	合計
男	60	30	90
女	90	20	110
合計	150	50	200

則

所以可以在犯錯誤的概率不超過0.025的前提下認為“鍛煉達標”與性別有關；

（2）（ⅰ）在“鍛煉達標”的50名學生中，男、女生人數比為3：2，

所以用分層抽樣的方法抽出5人，男生有人，女生有人；

（ⅱ）參加體會交流的5人中，3名男生記為a，b，c，2名女生記為A，B，從中隨機選出3人作重點發言，一共有，，，，，，，，，10種不同的選法，其中選出的這3人中至少有1名女生的不同選法有，，，，，，，，9種，

故所求的概率為