
(本小題滿分10分)
如圖,平面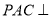 平面
平面 為等邊三角形,
為等邊三角形, 分別是線段
分別是線段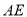 ,
,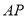 上的動點,且滿足:
上的動點,且滿足:
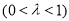 .
.

(Ⅰ)求證: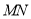 ∥平面
∥平面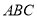 ;
;
(Ⅱ)當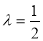 時,求平面ABC與平面MNC所成的銳二面角的大小.
時,求平面ABC與平面MNC所成的銳二面角的大小.
(Ⅰ)見解析;(Ⅱ)平面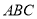 與平面
與平面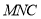 所成的銳二面角為
所成的銳二面角為 .
.
【解析】
試題分析:(Ⅰ)根據三角形相似性得到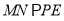 又因為
又因為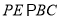 ,進而根據平行線的傳遞性得到
,進而根據平行線的傳遞性得到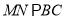 ,根據線面平行的判定定理得到證明; (Ⅱ)由(Ⅰ)知
,根據線面平行的判定定理得到證明; (Ⅱ)由(Ⅰ)知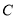 、
、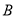 、
、 、
、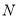 四點共面,且
四點共面,且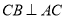 ,
,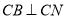 ,故所求的二面角即為
,故所求的二面角即為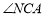 ,根據題中條件,進而進一步得到二面角的大小.
,根據題中條件,進而進一步得到二面角的大小.
試題解析:(Ⅰ)證明:由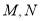 分別是線段
分別是線段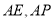 上的動點,且在
上的動點,且在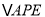 中,
中,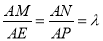
 ,得
,得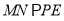 ,
,
又依題意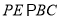 ,所以
,所以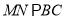 .
.
因為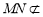 平面
平面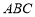 ,
,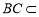 平面
平面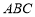 ,
,
所以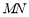 //平面
//平面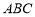 . 5分
. 5分
(Ⅱ)【解析】
由(Ⅰ)知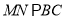 ,故
,故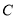 、
、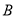 、
、 、
、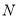 共面,
共面,
平面 與平面
與平面 所成的銳二面角即
所成的銳二面角即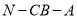 .
.
因為平面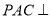 平面
平面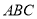 ,平面
,平面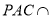 平面
平面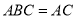 ,且
,且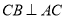 ,
,
所以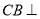 平面
平面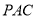 .故
.故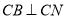 ,
,
即知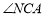 為二面角
為二面角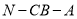 的平面角
的平面角
∵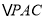 為等邊三角形,
為等邊三角形, 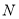 是線段
是線段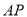 的中點,
的中點,
∴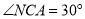
故平面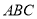 與平面
與平面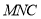 所成的銳二面角為
所成的銳二面角為 10分
10分
考點:1.線線平行,線面平行的判斷定理;2.四點共面的公理;3.求二面角的大小.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:高中數學 來源:2014-2015學年山東省棗莊市高三1月月考理科數學試卷(解析版) 題型:選擇題
已知某幾何體的三視圖(單位:cm)如圖所示,則該幾何體的體積是( )

A.48cm3 B.98cm3 C.88cm3 D.78cm3
查看答案和解析>>
科目:高中數學 來源:2014-2015學年浙江省杭州市高二11月月考數學試卷(解析版) 題型:填空題
設直線 的方程為
的方程為 ,將直線
,將直線 繞其與
繞其與 軸交點按逆時針方向旋轉90°得到直線
軸交點按逆時針方向旋轉90°得到直線 ,則
,則 的方程為 .
的方程為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com