
【題目】已知數列![]() 滿足
滿足![]() 。
。
(1)若![]() 成等比數列,求
成等比數列,求![]() 的值。
的值。
(2)是否存在![]() ,使數列
,使數列![]() 為等差數列?若存在,求出所有這樣的
為等差數列?若存在,求出所有這樣的![]() ;若不存在,說明理由。
;若不存在,說明理由。
【答案】(1)![]() 或
或![]() ;(2) 當且僅當
;(2) 當且僅當![]() 時,數列
時,數列![]() 為等差數列.
為等差數列.
【解析】
試題(1)把![]() 表示為
表示為![]() 的式子,通過對
的式子,通過對![]() 的范圍進行討論去掉絕對值符號,根據
的范圍進行討論去掉絕對值符號,根據![]() 成等比數列可得關于
成等比數列可得關于![]() 的方程,解出即可;
的方程,解出即可;
(2)假設這樣的等差數列存在,則![]() 成等差數列,即
成等差數列,即![]() ,將(1)的過程代入,得到關于
,將(1)的過程代入,得到關于![]() 的方程,分情況①當
的方程,分情況①當![]() 時②當
時②當![]() 時,求得
時,求得![]() 進行判斷;看是否與
進行判斷;看是否與![]() 矛盾.此題的難點在與討論絕對值的幾何意義,去絕對值.
矛盾.此題的難點在與討論絕對值的幾何意義,去絕對值.
試題解析:(1)∵![]() ,∴
,∴![]() ,
,![]() .
.
(ⅰ)當![]() 時,
時,![]() ,
,
由![]() ,
,![]() ,
,![]() 成等比數列得:
成等比數列得:
∴![]() ,解得
,解得![]() . 3分
. 3分
(ⅱ)當![]() 時,
時,![]()
∴![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() .
.
綜上可得![]() 或
或![]() . 6分
. 6分
(2)假設這樣的等差數列存在,則
由![]() ,得
,得![]() ,即
,即![]() .
.
(ⅰ)當![]() 時,
時,![]() ,解得
,解得![]() ,從而
,從而![]() (
(![]() ),此時
),此時![]() 是一個等差數列; 9分
是一個等差數列; 9分
(ⅱ)當![]() 時,
時,![]() ,解得
,解得![]() ,與
,與![]() 矛盾;
矛盾;
綜上可知,當且僅當![]() 時,數列
時,數列![]() 為等差數列. 12分
為等差數列. 12分


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:
【題目】某中學高三年級從甲、乙兩個班級各選出7名學生參加數學基本公式大賽,他們取得的成績(滿分100分)的莖葉圖如圖,其中甲班學生的平均分是85,乙班學生成績的中位數是83.
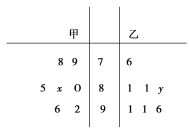
(1)求x和y的值;
(2)從成績在90分以上的學生中隨機抽取兩名學生,求甲班至少有一名學生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設整數![]() ,對置于
,對置于![]() 個點
個點![]() 及點
及點![]() 處的卡片作如下操作:操作
處的卡片作如下操作:操作![]() :若某個點
:若某個點![]() 處的卡片數不少于3,則可從中取出三張,在三點
處的卡片數不少于3,則可從中取出三張,在三點![]() 、
、![]() 、
、![]() 處各放一張
處各放一張![]() ;操作
;操作![]() :若點
:若點![]() 處的卡片數不少于
處的卡片數不少于![]() ,則可從中取出
,則可從中取出![]() 張,在
張,在![]() 個點
個點![]() 處各放一張。證明:只要放置于這
處各放一張。證明:只要放置于這![]() 個點處的卡片總數不少于
個點處的卡片總數不少于![]() ,則總能通過若干次操作,使得每個點處的卡片數均不少于
,則總能通過若干次操作,使得每個點處的卡片數均不少于![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用0,1,2,3,4,5這六個數字,完成下面三個小題.
(1)若數字允許重復,可以組成多少個不同的五位偶數;
(2)若數字不允許重復,可以組成多少個能被5整除的且百位數字不是3的不同的五位數;
(3)若直線方程![]() 中的a,b可以從已知的六個數字中任取2個不同的數字,則直線方程表示的不同直線共有多少條?
中的a,b可以從已知的六個數字中任取2個不同的數字,則直線方程表示的不同直線共有多少條?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}滿足an+1+(-1)n an =2n-1,則{an}的前64項和為( )
A. 4290 B. 4160 C. 2145 D. 2080
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 山東省《體育高考方案》于2012年2月份公布,方案要求以學校為單位進行體育測試,某校對高三1班同學按照高考測試項目按百分制進行了預備測試,并對50分以上的成績進行統計,其頻率分布直方圖如圖所示,若90~100分數段的人數為2人.
(Ⅰ)請估計一下這組數據的平均數M;
(Ⅱ)現根據初賽成績從第一組和第五組(從低分段到高分段依次為第一組、第二組、…、第五組)中任意選出兩人,形成一個小組.若選出的兩人成績差大于20,則稱這兩人為“幫扶組”,試求選出的兩人為“幫扶組”的概率.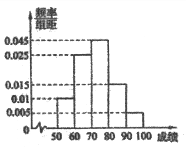
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com