
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{2}$ |
分析 由題意可知:雙曲線方程為:$\frac{{x}^{2}}{{c}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0),漸近線方程為y=±$\frac{b}{c}$x,圓心為(a,0),半徑為c,即d=$\frac{丨ab丨}{\sqrt{{b}^{2}+{c}^{2}}}$=b,即b=c,a=$\sqrt{2}$c,橢圓C的離心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
解答 解:由題意可知:橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),焦點在x軸上,a2=b2+c2,
雙曲線以橢圓C的焦點為頂點,頂點為焦點,
雙曲線方程為:$\frac{{x}^{2}}{{c}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0),漸近線方程為y=±$\frac{b}{c}$x,
圓M:(x-a)2+y2=c2,圓心為(a,0),半徑為c,
雙曲線的兩條漸近線都與圓M相切,則圓心到漸近線的距離d=c,
即d=$\frac{丨ab丨}{\sqrt{{b}^{2}+{c}^{2}}}$=b,即b=c,a=$\sqrt{2}$c,
橢圓C的離心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
故選A.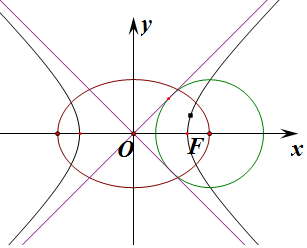
點評 本題考查橢圓的標準方程及簡單幾何性質,考查雙曲線的漸近線方程,點到直線的距離公式,考查數形結合思想,屬于中檔題.


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 實驗操作 | |||||
| 不合格 | 合格 | 良好 | 優秀 | ||
| 體 能 測 試 | 不合格 | 0 | 0 | 1 | 1 |
| 合格 | 0 | 2 | 1 | b | |
| 良好 | 1 | a | 2 | 4 | |
| 優秀 | 1 | 2 | 3 | 6 | |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,某幾何體的三視圖中,正視圖和側視圖都是半徑為$\sqrt{3}$的半圓和相同的正三角形,其中三角形的上頂點是半圓的中點,底邊在直徑上,則它的表面積是( )
如圖,某幾何體的三視圖中,正視圖和側視圖都是半徑為$\sqrt{3}$的半圓和相同的正三角形,其中三角形的上頂點是半圓的中點,底邊在直徑上,則它的表面積是( )| A. | 6π | B. | 8π | C. | 10π | D. | 11π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
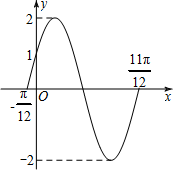 若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分圖象如圖所示.
若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
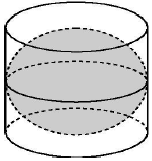 如圖是古希臘數學家阿基米德的墓碑文,墓碑上刻著一個圓柱,圓柱內有一個內切球,這個球的直徑恰好與圓柱的高相等.相傳這個圖形表達了阿基米德最引以自豪的發現.我們來重溫這個偉大發現.經計算球的體積等于圓柱體積的$\frac{2}{3}$倍.
如圖是古希臘數學家阿基米德的墓碑文,墓碑上刻著一個圓柱,圓柱內有一個內切球,這個球的直徑恰好與圓柱的高相等.相傳這個圖形表達了阿基米德最引以自豪的發現.我們來重溫這個偉大發現.經計算球的體積等于圓柱體積的$\frac{2}{3}$倍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com