
【題目】如圖,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,長軸長為4,
,長軸長為4,![]() 、
、![]() 分別是橢圓
分別是橢圓![]() 的左、右頂點,過右焦點
的左、右頂點,過右焦點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.

(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)記![]() 、
、![]() 的面積分別為
的面積分別為![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(Ⅲ)設線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,記直線
,記直線![]() 、
、![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() 、
、![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(Ⅰ)根據長軸長、離心率和橢圓![]() 關系可求得
關系可求得![]() ,進而得到橢圓方程;
,進而得到橢圓方程;
(Ⅱ)由面積比可得到![]() ,由此利用
,由此利用![]() 表示出
表示出![]() ,根據兩點在橢圓上,代入整理求得
,根據兩點在橢圓上,代入整理求得![]() ,進而得到所求斜率;
,進而得到所求斜率;
(Ⅲ)利用點差法可求得![]() ,求得
,求得![]() 點坐標后可得到
點坐標后可得到![]() ;將直線方程與橢圓方程聯立后可求得
;將直線方程與橢圓方程聯立后可求得![]() 坐標,由三點共線可整理得到
坐標,由三點共線可整理得到![]() ,進而得到
,進而得到![]() ;將上述三個關系式代入
;將上述三個關系式代入![]() 整理可得最終結果.
整理可得最終結果.
(Ⅰ)設橢圓的焦距為![]() ,
,
![]() 橢圓長軸長為
橢圓長軸長為![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() 橢圓
橢圓![]() 的標準方程為
的標準方程為![]() ;
;
(Ⅱ)設點![]() ,
,![]() .
.
![]() ,
,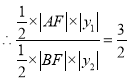 ,又
,又![]() ,
,![]() ,
, ,
,
![]() ,代入坐標可得:
,代入坐標可得: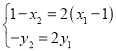 ,即
,即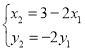 ,
,
又點![]() 、
、![]() 在橢圓
在橢圓![]() 上,
上,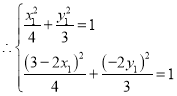 ,解得:
,解得: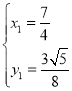 ,
,
![]() 直線
直線![]() 的斜率
的斜率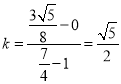 ;
;
(Ⅲ)![]() 點
點![]() ,
,![]() 在橢圓
在橢圓![]() 上,
上,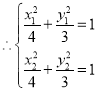 ,
,
兩式相減得:![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,
,![]() 直線
直線![]() 的方程為
的方程為![]() ,
,
令![]() 得:
得:![]() ,即
,即![]() ,
,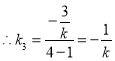 ,
,
又直線![]() 的方程為
的方程為![]() ,
,
與橢圓![]() 聯立
聯立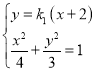 整理得:
整理得:![]() ,
,
![]() ,解得:
,解得:![]() ,
,![]() ,
,
![]() 點
點![]() 的坐標為
的坐標為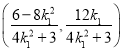 ,同理可得:點
,同理可得:點![]() 的坐標為
的坐標為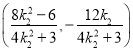 .
.
又點![]() 、
、![]() 、
、![]() 三點共線,
三點共線, ,
,
整理得:![]() ,
,
由題意知:![]() ,
,![]() ,
,![]() ,
,
由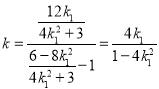 可得:
可得:![]() ,即
,即![]() .
.
![]() .
.


 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:高中數學 來源: 題型:
【題目】數![]() (其中
(其中![]() )的圖象如圖所示,為了得到
)的圖象如圖所示,為了得到![]() 的圖象,則只要將
的圖象,則只要將![]() 的圖象上所有的點( )
的圖象上所有的點( )

A.向左平移![]() 個單位長度,縱坐標縮短到原來的
個單位長度,縱坐標縮短到原來的![]() ,橫坐標不變
,橫坐標不變
B.向左平移![]() 個單位長度,縱坐標伸長到原來的3倍橫坐標不變
個單位長度,縱坐標伸長到原來的3倍橫坐標不變
C.向右平移![]() 個單位長度,縱坐標縮短到原來的
個單位長度,縱坐標縮短到原來的![]() ,橫坐標不變
,橫坐標不變
D.向右平移![]() 個單位長度,縱坐標伸長到原來的3倍,橫坐標不變
個單位長度,縱坐標伸長到原來的3倍,橫坐標不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以O為極點,x軸正半軸為極軸建立極坐標系,直線l的參數方程為![]() (t為參數),曲線C1的方程為ρ(ρ-4sin θ)=12,定點A(6,0),點P是曲線C1上的動點,Q為AP的中點.
(t為參數),曲線C1的方程為ρ(ρ-4sin θ)=12,定點A(6,0),點P是曲線C1上的動點,Q為AP的中點.
(1)求點Q的軌跡C2的直角坐標方程;
(2)直線l與直線C2交于A,B兩點,若|AB|≥2![]() ,求實數a的取值范圍.
,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年,河南省鄭州市的房價依舊是鄭州市民關心的話題.總體來說,二手房房價有所下降,相比二手房而言,新房市場依然強勁,價格持續升高.已知銷售人員主要靠售房提成領取工資.現統計鄭州市某新房銷售人員一年的工資情況的結果如圖所示,若近幾年來該銷售人員每年的工資總體情況基本穩定,則下列說法正確的是( )

A.月工資增長率最高的為8月份
B.該銷售人員一年有6個月的工資超過4000元
C.由此圖可以估計,該銷售人員2020年6,7,8月的平均工資將會超過5000元
D.該銷售人員這一年中的最低月工資為1900元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖在矩形ABCD中,AB=5,AD=2,點E在線段AB上,且BE=1,將△ADE沿DE折起到A1DE的位置,使得平面A1DE⊥平面BCDE.
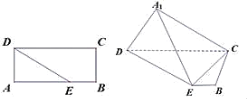
(1)求證:CE⊥平面A1DE;
(2)線段A1C上是否存在一點F,使得BF//平面A1DE?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖和90后從事互聯網行業者崗位分布圖(90后指1990年及以后出生,80后指1980-1989年之間出生,80前指1979年及以前出生),則下列結論中不一定正確的是( )
整個互聯網行業從業者年齡分布餅狀圖 90后從事互聯網行業者崗位分布圖


A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數90后比80后多
C.互聯網行業中從事設計崗位的人數90后比80前多
D.互聯網行業中從事市場崗位的90后人數不足總人數的10%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】投到某出版社的稿件,先由兩位初審專家進行評審,若能通過兩位初審專家的評審,則直接予以錄用,若兩位初審專家都未予通過,則不予錄用,若恰能通過一位初審專家的評審,則再由第三位專家進行復審,若能通過復審專家的評審,則予以錄用,否則不予錄用.設稿件能通過各初審專家評審的概率均為![]() ,復審的稿件能通過評審的概率為
,復審的稿件能通過評審的概率為![]() ,各專家獨立評審,則投到該出版社的1篇稿件被錄用的概率為__________.
,各專家獨立評審,則投到該出版社的1篇稿件被錄用的概率為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com