Question

已知等差數列{a_n}的首項a₁=1,公差d>0，且第2項，第5項，第14項分別是等比數列{b_n}的第2項，第3項，第4項．

（1）求數列{a_n}與{b_n}的通項公式；

 (2)求數列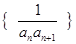的前n項和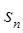

（3）設數列{c_n}對任意自然數n，均有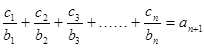，求c₁+c₂+c₃+……+c₂₀₀₆值．

 

Answer 1

【答案】

（1）a_n=2n-1,b_n=3^n-1.（2）見解析

（3）當n=1時，c₁=3 當n≥2時， ，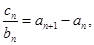

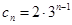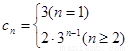
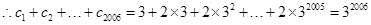
【解析】

試題分析：（1）利用等差數列的通項公式將第二項，第五項，第十四項用{a_n}的首項與公差表示，再據此三項成等比數列，列出方程，求出公差，利用等差數列及等比數列的通項公式求出數列{a_n}與{b_n}的通項公式．

（2）根據數列的通項公式通過裂項求解數列的和

（3）當n≥2時，根據a_n+1-a_n，求出數列{c_n}通項公式，但當n=1時，不符合上式，因此數列{c_n}是分段數列；然后根據通項公式即可求出結果

解：（1）由題意得（a₁+d）(a₁+13d)=(a₁+4d)²(d>0)  解得d=2,∴a_n=2n-1,b_n=3^n-1.

（3）當n=1時，c₁=3 當n≥2時， ，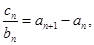

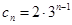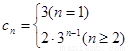
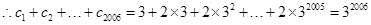
考點：本試題主要考查了利用基本量表示等差數列、等比數列的通項，疊加求解數列的通項．

點評：解決該試題的關鍵是對于等差數列，等比數列基本關系式的求解和運用。